Trig Substitution Cheat Sheet is a technique used in solving integrals involving algebraic functions with certain types of expressions. It involves replacing these expressions with the ratios of trigonometric functions.

Trig Substitution Cheat Sheet
This substitution allows one to evaluate integrals that would otherwise difficult or impossible to solve.
Here a cheat sheet of the most common trigonometry substitution formulas:
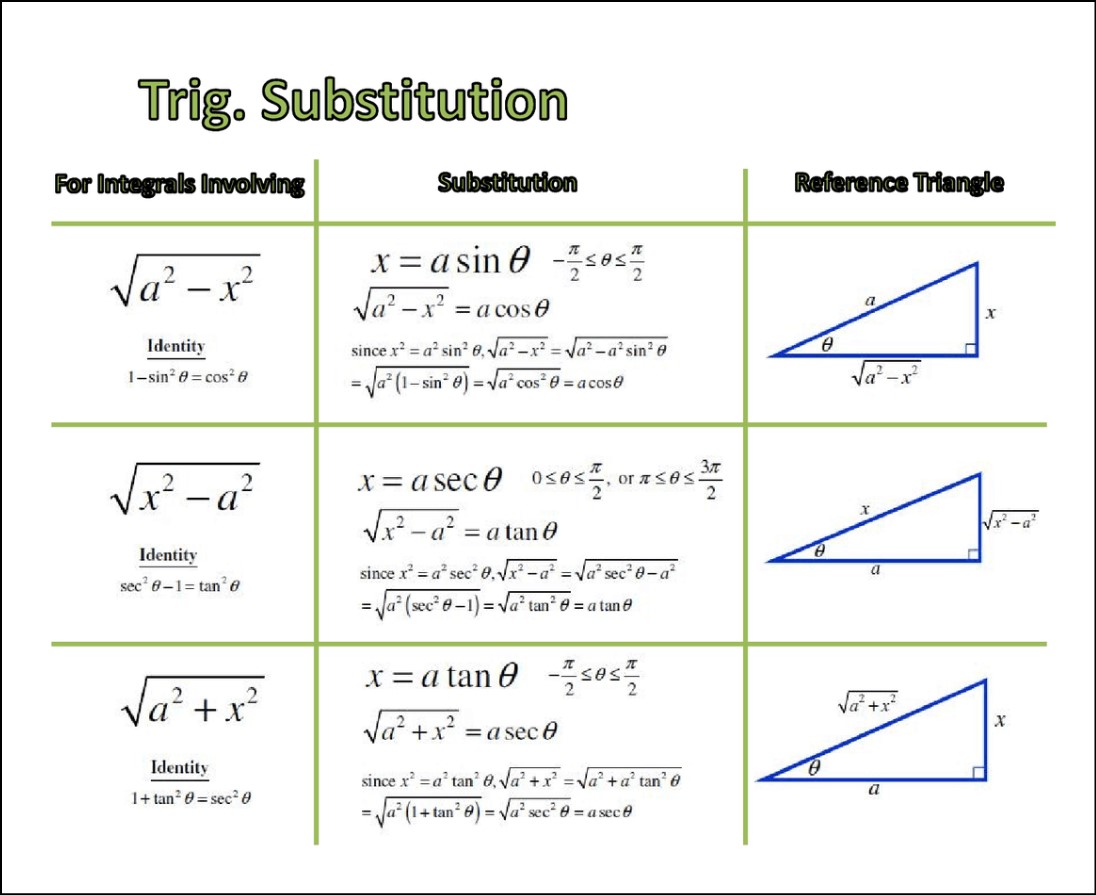
√(a^2 – x^2) = sinθ
Where a is a constant, x is the variable being integrated, and θ is the angle whose sine is equal to x/a.
√(x^2 – a^2) = cosθ
Where a is a constant, x is the variable being integrated, and θ is the angle whose cosine is equal to x/a.
√(x^2 + a^2) = tanθ
Where a is a constant, x is the variable being integrated, and θ is the angle whose tangent is equal to x/a.
x = a tanθ
Where a is a constant, x is the variable being integrated, and θ is the angle whose tangent is equal to x/a.
x = a secθ
Where a is a constant, x is the variable being integrated, and θ is the angle whose secant is equal to x/a.
x = a cscθ
Where a is a constant, x is the variable being integrated, and θ is the angle whose cosecant is equal to x/a.
Trigonometry Substitution Cheat Sheet
When making a trigonometric substitution, it important to remember the following steps:
Identify the expression that can substituted with a trigonometric function. Choose the appropriate trigonometric function based on the expression.
Replace the expression with the corresponding trigonometric function and determine the value of θ.
Make the substitution and integrate.
Check the solution to see if it the most simplified form possible.
There some general guidelines for when to use trigonometric substitution. It most useful when the integrand involves expressions that of the form √(a^2 – x^2), √(x^2 – a^2), or √(x^2 + a^2). These expressions often encountered when integrating functions that involve squares or square roots.
Here some examples of how to use trigonometric substitution:
Example 1: Evaluate the integral of √(9 – x^2) dx.
Solution: Identify the expression that can substituted with a trigonometric function.
In this case, the expression √(9 – x^2).
Choose the appropriate trigonometric function based on the expression.
Since the expression of the form √(a^2 – x^2), it can substituted with sinθ.
Replace the expression with the corresponding trigonometric function and determine the value of θ.
In this case, θ = sin^-1 (x/3).
Make the substitution and integrate.
∫ √(9 – x^2) dx
It also important to note that trigonometric substitution not always the best method for evaluating integrals. In some cases, it may more appropriate to use other techniques, such as partial fraction decomposition or substitution with substitution. Check out other posts:- Hyperbolic Trig Identity, Trig Reciprocal Identities With Formula.
Trigonometry Substitution Cheat Sheet
-
Pythagorean Identities:
- sin^2(x) + cos^2(x) = 1
- 1 + tan^2(x) = sec^2(x)
- 1 + cot^2(x) = csc^2(x)
-
Trigonometric Substitutions:
- For sqrt(a^2 – x^2), substitute x = a*sin(theta)
- For sqrt(x^2 + a^2), substitute x = a*tan(theta)
- For sqrt(x^2 – a^2), substitute x = a*sec(theta)
- For 1/sqrt(a^2 – x^2), substitute x = a*sin(theta)
- For 1/sqrt(x^2 + a^2), substitute x = a*tan(theta)
- For 1/sqrt(x^2 – a^2), substitute x = a*sec(theta)
-
Trigonometric Identities:
- sin(2theta) = 2*sin(theta)*cos(theta)
- cos(2theta) = cos^2(theta) – sin^2(theta)
- tan(2theta) = 2*tan(theta) / (1 – tan^2(theta))
- sin(theta) = cos(90 – theta)
- cos(theta) = sin(90 – theta)
- tan(theta) = 1 / cot(theta)
- sec(theta) = 1 / cos(theta)
- csc(theta) = 1 / sin(theta)
- cot(theta) = 1 / tan(theta)
These substitutions useful when solving integrals or differential equations involving trigonometric functions. However, it’s important to note that the choice of substitution may vary depending on the specific problem you’re solving.