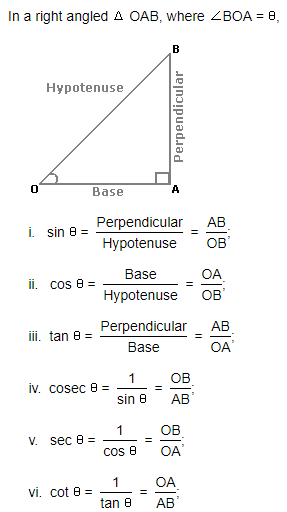
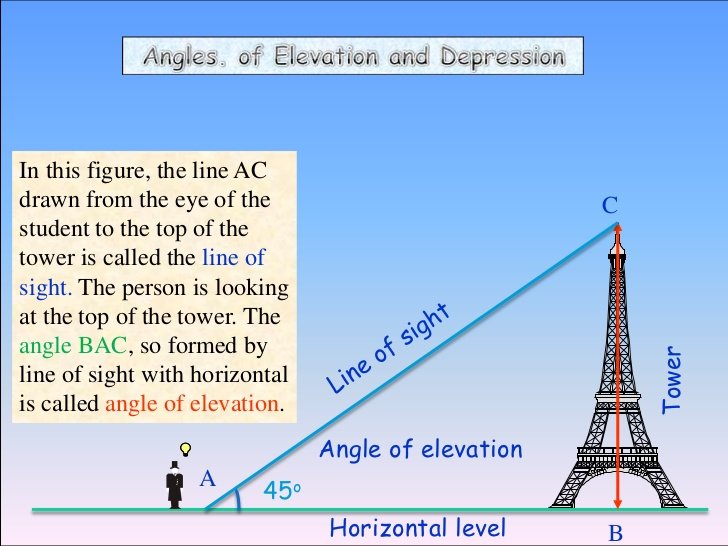
Height and Distance: The subject trigonometry deals with the study of finding the relationship between the angle of a triangle and the length of its side. A triangle is a closed shape that represents three sides.
- Integration Formula
- Formula of Trigonometry
- Trigonometric Ratios
- Trigonometric functions with Formulas
- What are Trigonometric derivatives
- Trig Identities
- Height and distance
- Trigonometry formula Involving Sum Difference Product Identities
- Pythagorean Theorem
- Differentiation Formula
- Basic Trig Identities

Definition of Height and Distance
Before understanding the method of calculating height and distance, it is necessary to know the definition of height and distance separately. Height is defined as the measurement of an object in the vertical direction. Distance is considered as the measurement of an object from a specific point in the horizontal direction.
How do you Calculate Height and Distance?
The calculation of the height of an object is achieved by the measurement of its distance from the object. This includes the angle of elevation at the top of the object while calculating the height. The tangent of the angle is considered as the height of the object, which is divided by the distance from the object. From this calculation, the height of the object is evaluated.
By observing the above figure, one can consider that an observer is located at point C. Here, the height of the object is exhibited by the line AB. The distance between the object and the observer is shown by the line BC. It can be seen that the object may or may not be perpendicular to the ground. From the figure, the line AC is considered as the line of sight or imaginary line, while the observer is viewing the topmost point of the object. Further, it may be seen that angle β signifies the angle of depression. Similarly, the angle α denotes the angle of elevation.
How do you find height with angle and distance?
If the student is provided with any of the two quantities, which may be a side or an angle, it is possible for him/her to evaluate the rest of the quantities. Here, usage of trigonometry comes into picture. Through the law of alternate angle, it may be seen that the angle of depression and elevation are apparently found to be equal in magnitude, which means α = β. Further, it can be found that Tan α is equivalent to ratio of the height and distance.
From the above figure, if the student is provided with any two of the following data, such as the angle of depression or angle of elevation and distance, it is possible to calculate the height.
Height and Distance Worksheet