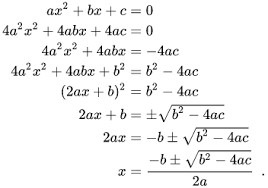In elementary algebra, the Sri Dharacharya formula is something that solves most of the algebraic problems. If you have studied the middle and advanced stage of Algebra then you must have come across the usage of the Dharacharya formula.
- Integration Formula
- Formula of Trigonometry
- Trigonometric Ratios
- Trigonometric functions with Formulas
- What are Trigonometric derivatives
- Heights and distance
- Trigonometry formula Involving Sum Difference Product Identities
- Trig Identities
- Pythagorean Theorem
- Differentiation Formula
- Basic Trig Identities
This particular formula is extremely useful in solving the quadratic equation of Algebra. With this formula, one can easily solve the equation by finding the roots of the equation in prompt timings. This is the reason that why the Dharacharya formula is so relevant and significant in the domain of Elementary Algebra.
Quadratic Equation Vs Dharacharya Formula
Well, as we have just discussed that Dharacharya Method is primarily concerned with the Quadratic equation. It’s therefore significant to understand the Quadratic equation so as to understand the application of the Dharacharya formula into this equation.
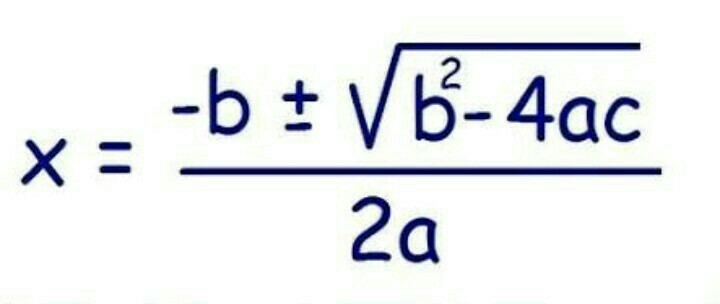
In elementary algebra, a quadratic equation is an equation that has the form of ax^2 + bx + c=0. Here in this equation X remains the unknown while the a,b and c have their own specific values. Here we have to determine the value of x by solving this whole equation and that’s where the role of the Dharacharya formula comes into play.
With the application of this formula, we can easily solve this whole equation and get the values of x. Remember the Dharacharya formula is only applicable to the Quadratic equations hence the equation must be quadratic.
Sri Dharacharya Formula
The Dharacharya formula is quite simple to use in order to solve the equation quickly and with utmost accuracy. The formula is written as x=−b±√b2−4ac2a where you just need to place the respective values in order to determine x. Subsequently, the real value of the x is known as the roots of the equation and these roots must satisfy the whole equation.
With the Dharacharya formula, you will always get the two answers to the quadratic equation. If both of the answers cease to satisfy the equation then there always comes the complex solution of the equation. In this quadratic equation the a,b and c are the coefficients of the x.
If the quadratic equation gets only one solution or the double root then we need to factor the equation further. There are some other ways as well to solve the quadratic equation however yet the Dharacharya formula is probably the best one. So, you can definitely use the Dharacharya formula for your personal purpose to solve the quadratic equation.