The inverse trigonometric function graph is something that you will most probably encounter while you studying. You will also encounter various problems based on the concept of inverse trigonometric functions.
Here in the article ahead, we are going to make our discussion specifically on this concept of inverse trigonometric functions. So we urge you to go through the entire article in order to have a decent understanding of inverse trigonometric functions for yourself.
Inverse Trigonometric Function Graph
Well, most of us are aware of the trigonometric functions which are the key foundation of how trigonometry works. These functions are the sine,cosine,tangent,secant,cosecant and cotangent. So basically the inverse trigonometric functions are just the opposite of common trigonometric functions that we have just mentioned above. In general terminology, we also know the inverse trigonometric functions as the arcus or cyclometric functions.
With the inverse trigonometric functions, you can calculate the angels with the given trigonometric ratios. The major application of inverse trigonometric functions lies in the domain of engineering, navigation, physics, etc.
Inverse Trig Functions Graph
Well, as you might be aware the trigonometric functions are directly associated with the right angle triangle. In fact, these functions are directly responsible to calculate the various measures of the triangle. For instance when you have the two known sides of the triangle then you can calculate the third side with the help of functions.
So, basically when we talk about the inverse trigonometric functions then we get to have different functions. The inverse trigonometric functions become as arcsine,arccosine,arctangent,arccotangent,arccosecant. You can clearly observe here that why we know the inverse trigonometric functions as the “arc” functions. In a similar manner, the derivatives of the inverse trigonometric functions also change their forms.
Graphic Representation Inverse of Trigonometric Functions
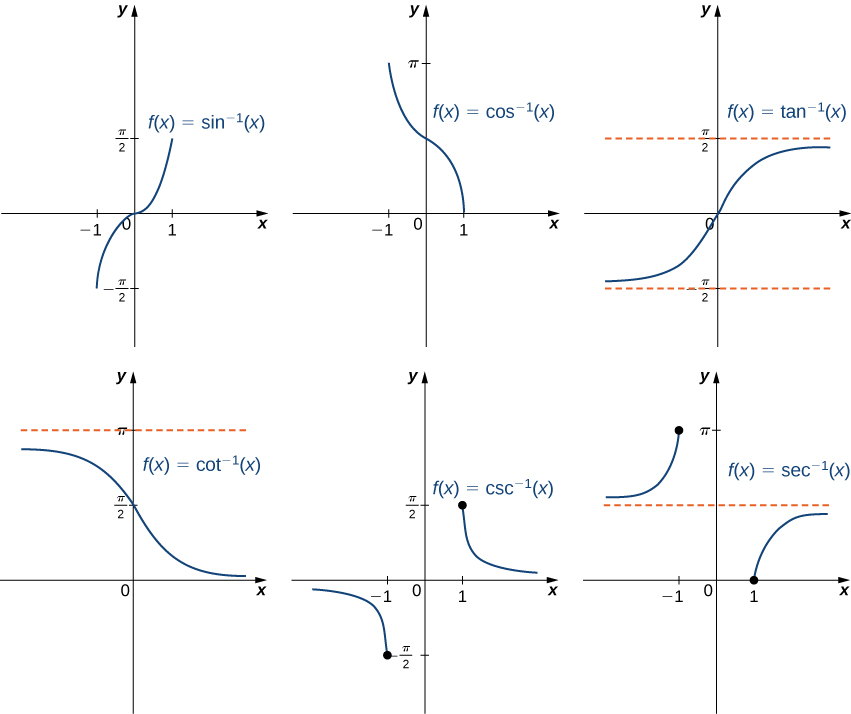
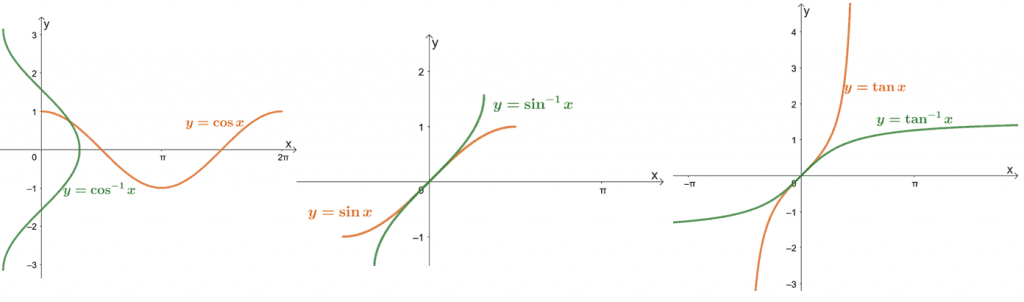
If you are facing difficulty in understanding the inverse trigonometric functions then you can check out the graphical representation of it. It will guide you in understanding each inverse trigonometric function in a systematic manner. The graphical representation basically states the derivation of an inverse function from the straight functions.
The graphical representation, therefore, becomes extremely helpful in having a thorough understanding of trigonometric functions. For instance, the sine function in its inverse form is denoted by the cos^-1x and in a similar manner, other functions also change their forms. The graphical representation of the inverse trigonometric functions comes very handy to learn all the inverse functions.
FAQ related to Inverse Trigonometric Function Graph – Sin, Cos, Tan
Q: What are inverse trigonometric functions?
A: Inverse trigonometric functions are functions that calculate the angle measure when given a trigonometric ratio. The most commonly used inverse trigonometric functions are the inverse sine (sin^-1), inverse cosine (cos^-1), and inverse tangent (tan^-1).
Q: What is the domain and range of inverse trigonometric functions?
A: The domain of inverse trigonometric functions depends on the specific function, but typically ranges from -1 to 1. The range of inverse trigonometric functions is usually between -π/2 to π/2 for the inverse sine and cosine functions, and between -π/2 to π/2 for the inverse tangent function.
Q: How do you graph inverse trigonometric functions?
A: To graph inverse trigonometric functions, first determine the domain and range of the specific function. Then, plot key points on the graph, including the minimum and maximum values for the domain and range. Finally, connect the points with a smooth curve.
Q: What is the relationship between inverse trigonometric functions and their corresponding trigonometric functions?
A: Inverse trigonometric functions are the inverse of their corresponding trigonometric functions. For example, the inverse sine function (sin^-1) is the inverse of the sine function (sin). This means that if y = sin(x), then x = sin^-1(y).
Q: What are the properties of inverse trigonometric functions?
A: Some properties of inverse trigonometric functions include:
- The domain of an inverse trigonometric function is limited to certain values.
- The range of an inverse trigonometric function is limited to certain values.
- The inverse sine and cosine functions are even functions, while the inverse tangent function is an odd function.
- The inverse sine and cosine functions have a period of 2π, while the inverse tangent function has a period of π.
Q: How are inverse trigonometric functions used in real life?
A: Inverse trigonometric functions are used in a variety of fields, including physics, engineering, and navigation. For example, they can be used to calculate the angles of elevation and depression, the lengths of sides of a triangle, and the position and velocity of objects moving in circular paths.