Differentiation Formula: In mathematics, differentiation is a well-known term, which is generally studied in the domain of the calculus portion of mathematics. We all have studied and solved several problems in our high school and +2 levels.
- Integration Formula
- Formula of Trigonometry
- Trigonometric Ratios
- Trigonometric functions with Formulas
- What are Trigonometric derivatives
- Heights and distance
- Trigonometry formula Involving Sum Difference Product Identities
- Pythagorean Theorem
- Differentiation Formula
- Trig Identities
- Basic Trig Identities
Differentiation Formula for Trigonometric Functions
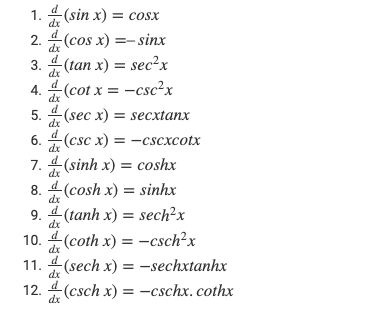
Differentiation Formulas for Inverse Trigonometric Functions
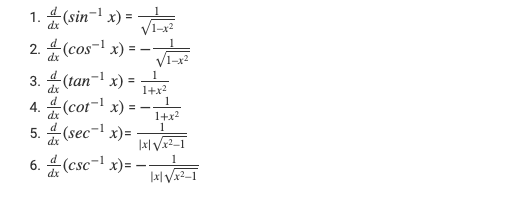
Other Differentiation Formula
In the language of laymen, differentiation can be explained as the measure or tool, by which we can measure the exact rate of change. For instance, you can figure out the rate of change in velocity, by the time for the given number of functions.
Well, if you are a math fanatic and want to solve several questions based on differentiation, then here we will help you with it.
We will discuss the systematic formula of differentiation by which you can determine the rate of speed for such function.
Types of Differential Equations
Differential equations can be divided into types which name are —
- Ordinary Differential Equations
- Partial Differential Equations
- Linear Differential Equations
- Non-linear differential equations
- Homogeneous Differential Equations
- Non-homogenous Differential Equations
Different Differentiation Formula for Calculus
Well, differentiation being the part of calculus may be comprised of several problems and for each problem, we have to apply a different set of formulas for its calculation.
So, if you want to have a solid grip and understanding of differentiation, then you must be having all its formulas in your head.
Here below is the list of several Differentiation formulas starting from the basic level and going to the advanced stage.
The derivative of the Exponential and Logarithmic functions
Recall the definition of the logarithm function with base a > 0 (with
Well, as we know that calculus is based on purely scientific calculations, where you have to apply a certain formula, to get the solution to a certain problem.
Similarly, you will encounter several problems in differentiation, for which you will be needing its specific formula to get the right answer.
There are several formulas in calculus and you have to apply the right formula to the concerned differential problem. We urge you to practice all the above-mentioned formulas to get better at solving differentiation problems.
FAQs related to differentiation formula of trigonometric functions.
Q: What are trigonometric functions?
A: Trigonometric functions are functions of an angle that are used to relate the angles of a triangle to the lengths of its sides. The most common trigonometric functions are sine, cosine, tangent, cotangent, secant, and cosecant.
Q: What is the differentiation formula for sine function?
A: The differentiation formula for sine function is:
d/dx(sin(x)) = cos(x)
Q: What is the differentiation formula for cosine function?
A: The differentiation formula for cosine function is:
d/dx(cos(x)) = -sin(x)
Q: What is the differentiation formula for tangent function?
A: The differentiation formula for tangent function is:
d/dx(tan(x)) = sec^2(x)
Q: What is the differentiation formula for cotangent function?
A: The differentiation formula for cotangent function is:
d/dx(cot(x)) = -csc^2(x)
Q: What is the differentiation formula for secant function?
A: The differentiation formula for secant function is:
d/dx(sec(x)) = sec(x)tan(x)
Q: What is the differentiation formula for cosecant function?
A: The differentiation formula for cosecant function is:
d/dx(csc(x)) = -csc(x)cot(x)




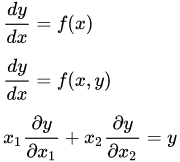
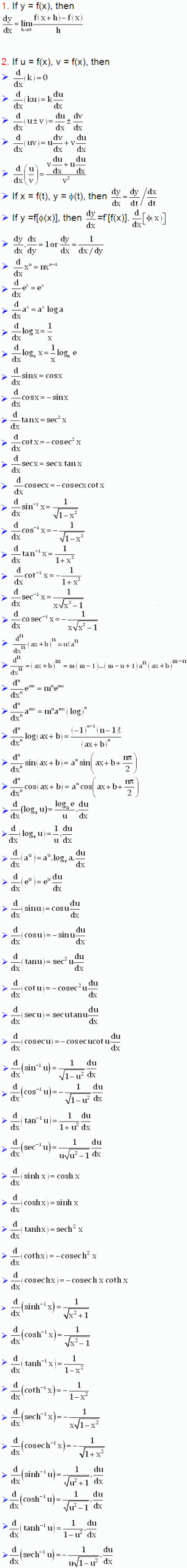

2sinx-1=
cos x
-sin x