The formula of Trigonometry: Trigonometry is a well-acknowledged name in the geometric domain of mathematics, which is in relevant in this domain for ages and is also practically applied across several occasions.
- Integration Formula
- Trig Identities
- Formula of Trigonometry
- Trigonometric Ratios
- Trigonometric functions with Formulas
- What are Trigonometric derivatives
- Heights and distance
- Trigonometry formula Involving Sum Difference Product Identities
- Pythagorean Theorem
- Differentiation Formula
- Basic Trig Identities
In simple language, trigonometry can be defined as that branch of algebra, which is concerned with the triangle. In this branch, we study the relationship between angles and the side length of a given triangle. With this detailed study of triangles, several types of equations are formed, which are consequently solved to simplify the relationship between the side and angle lengths of such triangles.
Trigonometry is considered one of the oldest components of Algebra, which has been existing around since the 3rd century. There are practical usages of trigonometry in several contexts such as in the domain of astronomy, surveying, optics, or periodic functions.
Formula of Trigonometry
Well, whether it is algebra or geometry both of these mathematics branches are based on scientific calculations of equations and we have to learn the different formulas to have easy calculations.
As we know that in Trigonometry we measure the different sides of a triangle, by which several equations are formed. Further, the formulas of Trigonometry are drafted following the various ratios used in the domain, such as sine, tangent, cosine, etc. So, there are the numbers of the formulas which are generally used in Trigonometry to measure the sides of the triangle.
Here below we are mentioning the list of different types of formulas for Trigonometry.
-
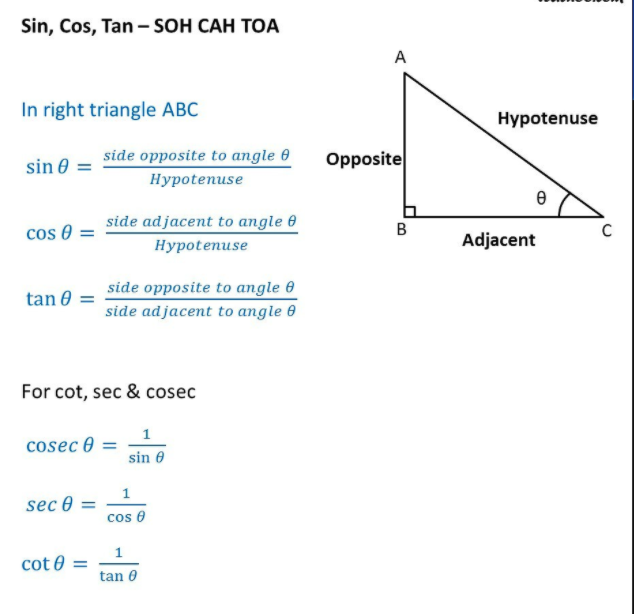
Trigonometry Basic Formula
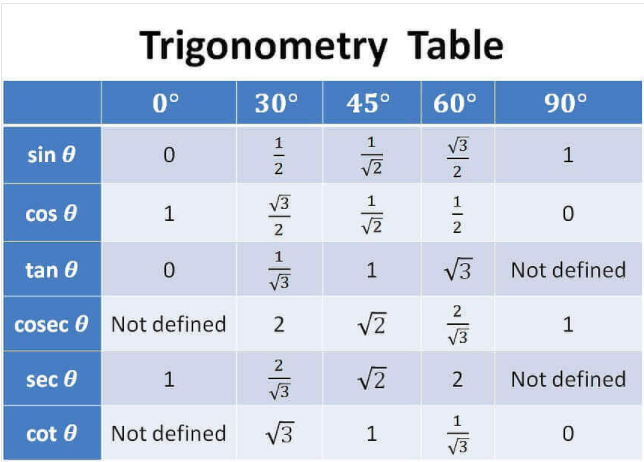
2. Sin Cos Tan at 0, 30, 45, 60 Degree
3. Pythagorean Identities
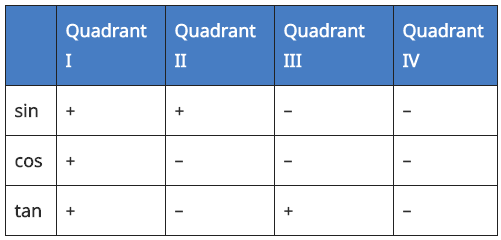
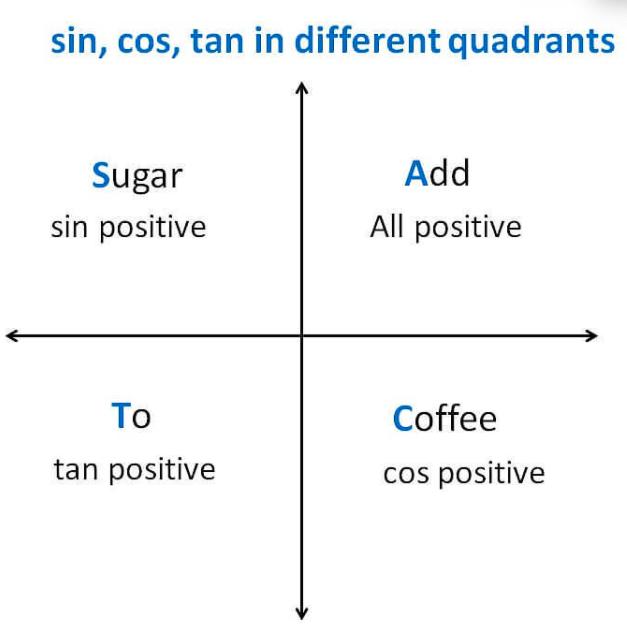
4. Sign of Sin, Cos, Tan in Different Quadrants
A dd– Sugar–To –Coffee
5. Radians
1 Degree = 60 Minutes
Ex: 1 °= 60′
1 Minute = 60 Seconds
Ex: 1′ = 60”
6. Negative Angles [Even-Odd Identies]
Sin (-x) = – Sin x
Cos (-x) = Cos x
Tan (-x) = – Tan x
Cot (-x) = – Cot x
Sec (-x) = Sec x
Cosec (-x) = – Cosec x
7. Value of Sin, Cos, Tan repeat after 2𝛑
Sin (2𝛑 + x) = Sin x
Cos (2𝛑 + x) = Cos x
Tan (2𝛑 + x) = Tan x
8. Periodicity Identities – Shifting Angles by 𝛑/2, 𝛑, 3𝛑/2
9. Angle Sum & Difference Identities
10. Double Angle Formula
11. Triple Angle Formula
12. Half Angle Identities
13. Sum Identities
14. Product Identities
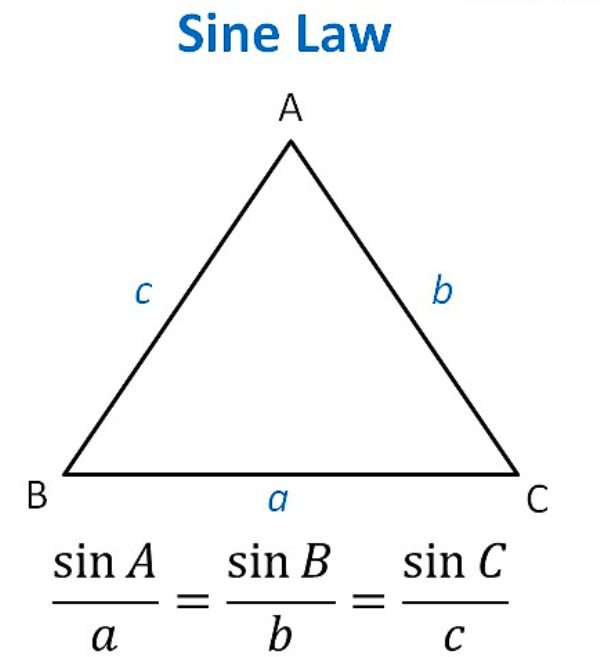
15. Law of Sin
Here,
- ABC are the vertices of the triangle ABC.
- The opposite site of angle A is a. i.e. BC
- The opposite site of angle B is b. i.e. AC
- The opposite site of angle C is c. i.e. AB
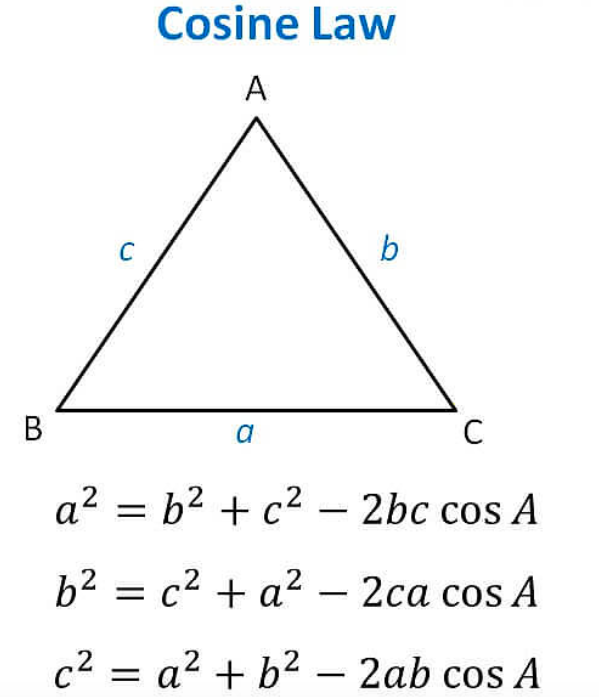
16. Law of Cosine
17. Inverse Trigonometric Function
If Sin θ = x
then Put Sin on the right side
So, By this, you can see that Sin is an angle, Same as Inverse of all Trignomentry function is an angle.
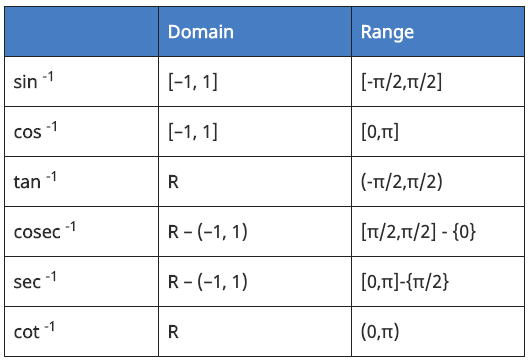
18. Domain and Range of Inverse Trigonometry Functions
19. Inverse Trigonometry Formula
20. Inverse Trigonometry Substitution
Just like any other branch of mathematics, the formulas of Trigonometry are equally important, since without these formulas you can’t put the values of triangles for the measurement purpose. These formulas are what simplifies the sides of triangles so that you can easily measure all their sides.
We urge all scholars to understand these formulas and then easily apply them to solve the various types of Trigonometry problems.
FAQs related to formulas of trigonometry
Q: What are the basic trigonometric functions?
A: The basic trigonometric functions are sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant (csc). These functions relate the ratios of the sides of a right-angled triangle to the angles in the triangle.
Q: What is the formula for sin?
A: The formula for sin is: sin(x) = opposite/hypotenuse, where x is the angle opposite to the side whose length is the “opposite” and the hypotenuse is the longest side of the right-angled triangle.
Q: What is the formula for cos?
A: The formula for cos is: cos(x) = adjacent/hypotenuse, where x is the angle adjacent to the side whose length is the “adjacent” and the hypotenuse is the longest side of the right-angled triangle.
Q: What is the formula for tan?
A: The formula for tan is: tan(x) = opposite/adjacent, where x is the angle opposite to the side whose length is the “opposite” and adjacent is the side next to it.
Q: What is the formula for cot?
A: The formula for cot is: cot(x) = adjacent/opposite, where x is the angle adjacent to the side whose length is the “adjacent” and opposite is the side next to it.
Q: What is the formula for sec?
A: The formula for sec is: sec(x) = hypotenuse/adjacent, where x is the angle adjacent to the side whose length is the “adjacent” and the hypotenuse is the longest side of the right-angled triangle.
Q: What is the formula for csc?
A: The formula for csc is: csc(x) = hypotenuse/opposite, where x is the angle opposite to the side whose length is the “opposite” and the hypotenuse is the longest side of the right-angled triangle.
Q: How are these trigonometric functions related to each other?
A: The functions sin, cos, tan, cot, sec, and csc are all related to each other through various trigonometric identities, such as the Pythagorean identity, reciprocal identities, quotient identities, and others.
Q: Can these trigonometric functions be used to solve real-world problems?
A: Yes, trigonometric functions are used extensively in fields such as physics, engineering, surveying, navigation, and many others to solve real-world problems related to angles, distances, and heights.



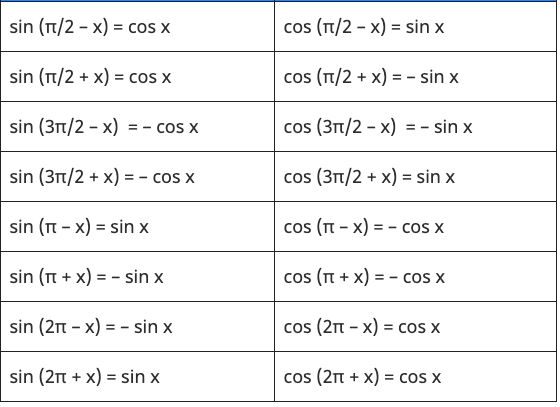
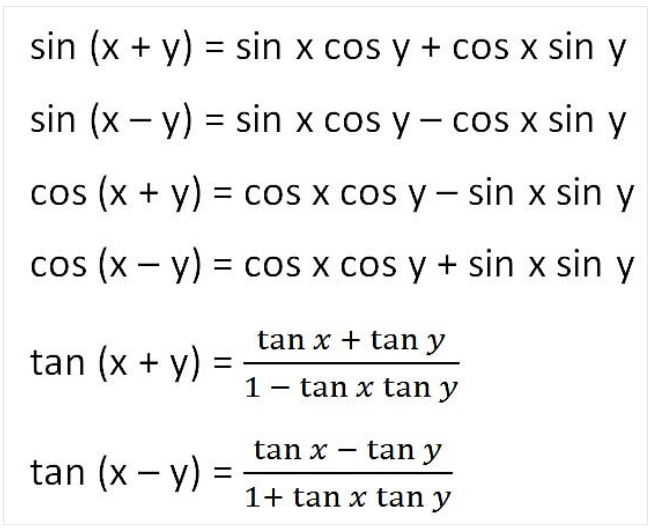
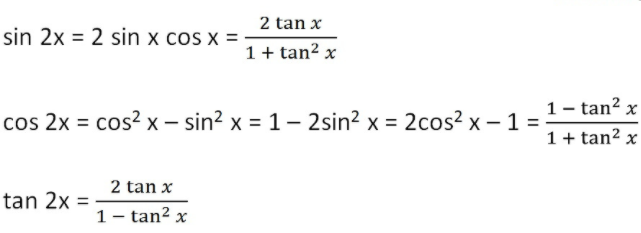
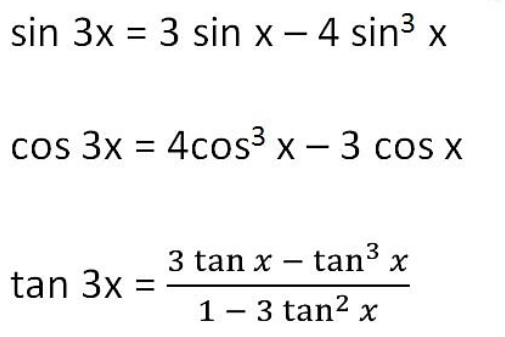
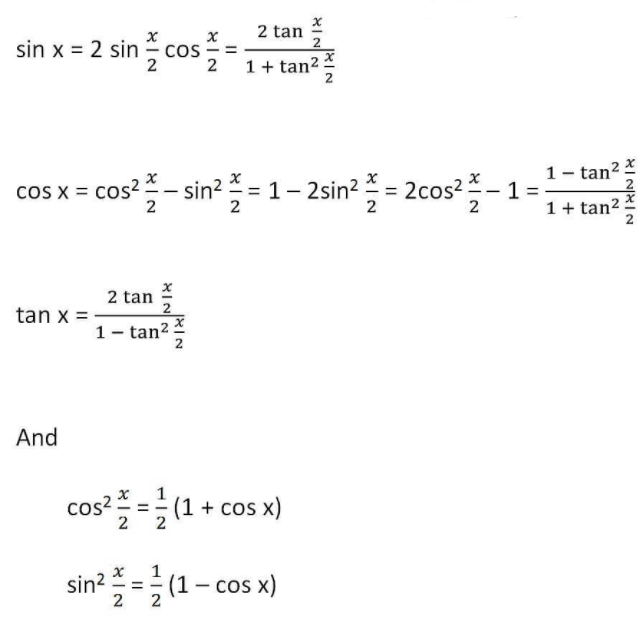
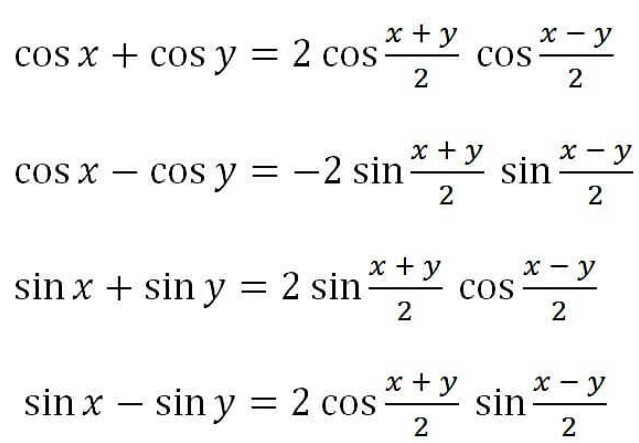

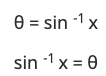
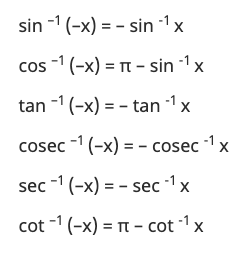
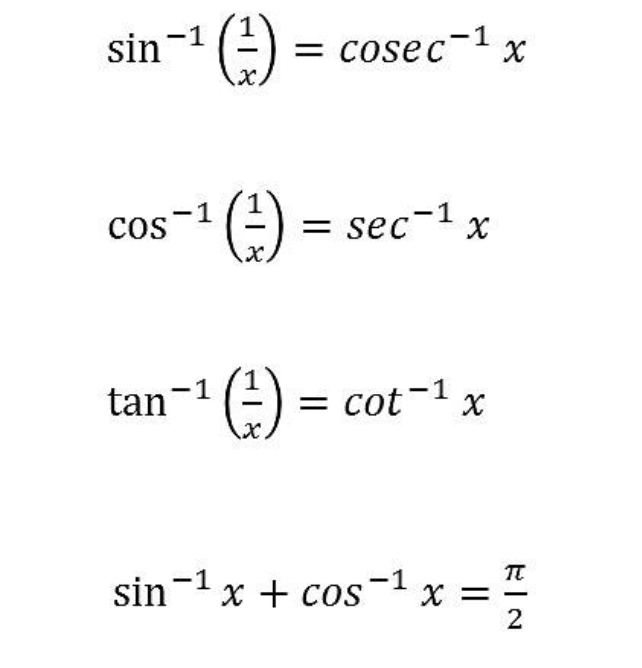
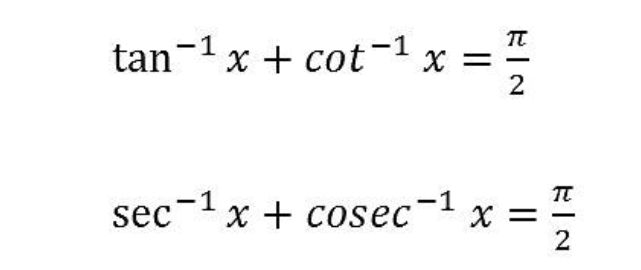
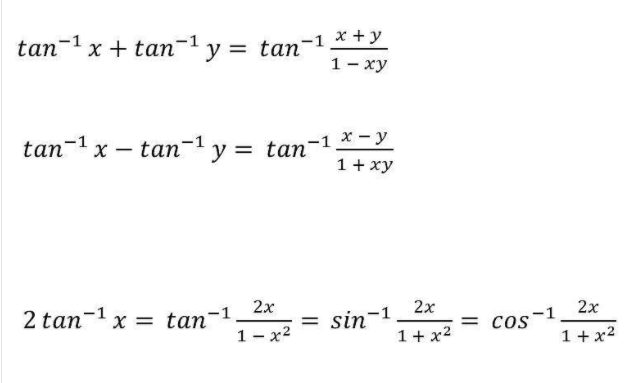

Hello, i would like to have some of the trigonometric notes in my email kindly. Otherwise its wow and i appreciate your good work done here for us the students engaging in mathematical studies.
Kindly i would like to have all the concepts in this area as well as calculus 1 as a university unit studied.
May God bless you abundantly.
Best regards from,
Odhiambo Stephen Otumba.
Sin cos tan cot sec cosece formula
Pandit badhri prsaad
Har har bhole
Sona chandhi tole
Sin=p/h
Cos =b/h
Tan =p/b
Cosec =h/p
Sec=h/b
Cot=b/p
Very nice
I want all formulas for class 11 and 12 maths; physics and chemistry cbse. Thankyou
Great!
Thanks
Great work bro..