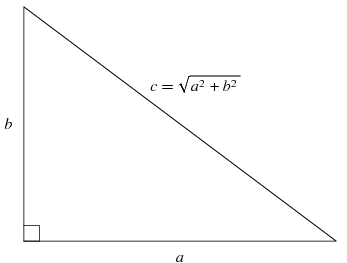
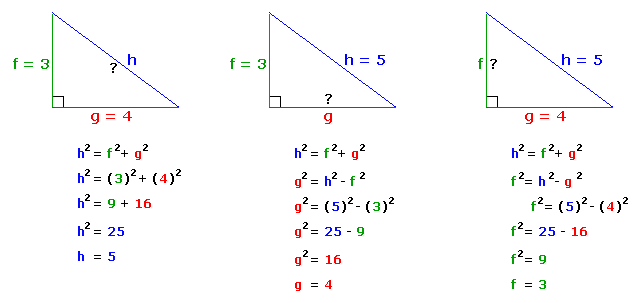The definition of the Pythagorean theorem is that in a right-angled triangle, the sum of the squares of the sides is equal to the square of the hypotenuse. It is important for students of mathematics to know that the Pythagorean theorem occupies great importance. They learn about this theorem in Algebra for the first time. But they find its actual usage in Calculus, Precalculus, Trigonometry, and Geometry.
- Integration Formula
- Formula of Trigonometry
- Trigonometric Ratios
- Trigonometric functions with Formulas
- What are Trigonometric derivatives
- Heights and distance
- Trigonometry formula Involving Sum Difference Product Identities
- Trig Identities
- Pythagorean Theorem
- Differentiation Formula
- Basic Trig Identities
Definition of Pythagorean Theorem
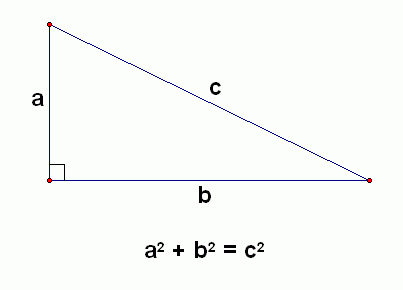
The credit with regard to Pythagorean theorem goes to philosopher and the famous Greek mathematician, named Pythagoras. According to early history, it is said that Babylonians were using it for the past 1500 years. However, the actual credit of proving it mathematically goes to Pythagoras only.
Further, the student should know that Pythagorean theorem is an important tool that can be used at all times while dealing with triangles. Irrespective of whichever mathematics class, the student will find its application for all the problems associated with triangles. In a simple way, the theorem states that it is a relationship that is established between the lengths of sides of a right-angled triangle. From this relationship it will be easy for the student to ascertain if a triangle is obtuse or acute.
Students should know that the theorem may have more proofs, which are known in comparison to any other like the law of quadratic reciprocity. It is important to mention here that a book has been published by name, The Pythagorean Proposition. Students referring to this book will find 370 proofs with regard to Pythagorean theorem.
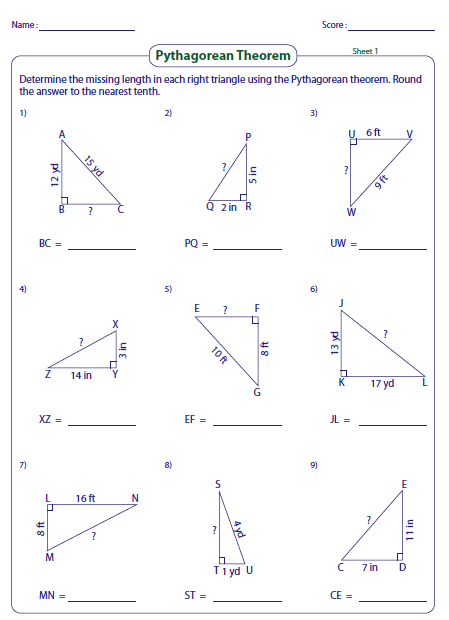
Pythagorean Theorem Worksheet
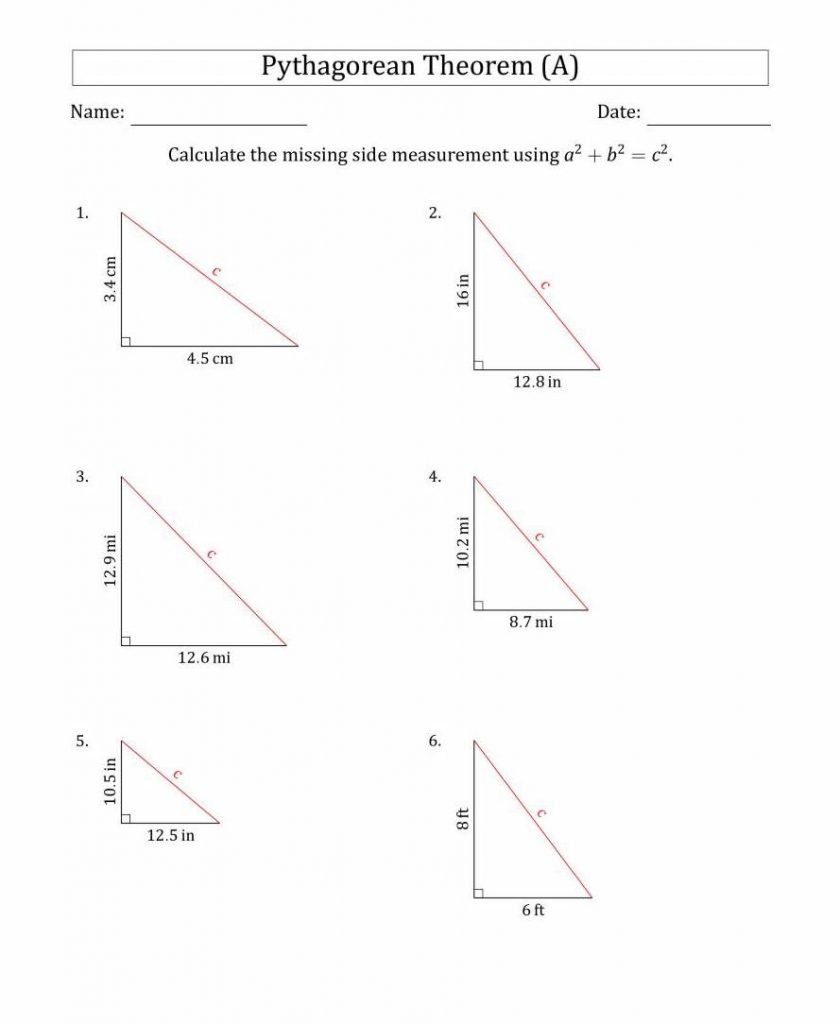
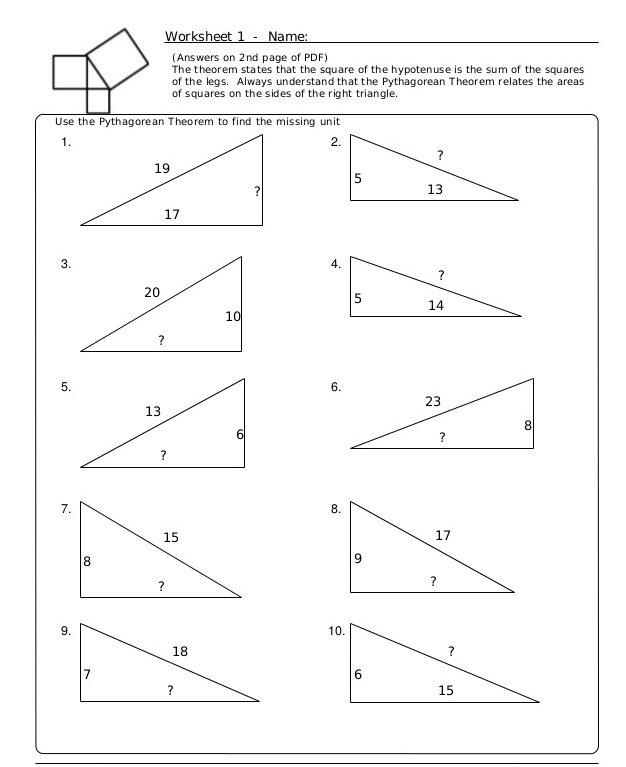
The proof of this theorem is based on the proportionality of the sides of two identical angles. This means that the ratio of any two corresponding two sides of identical triangles is considered the same. This is true irrespective of the size of the triangles under consideration.
Pythagorean Theorem with Examples