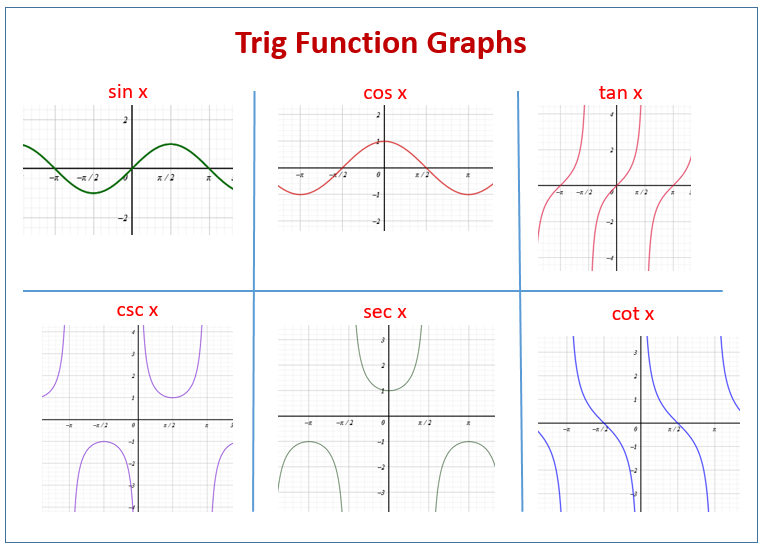
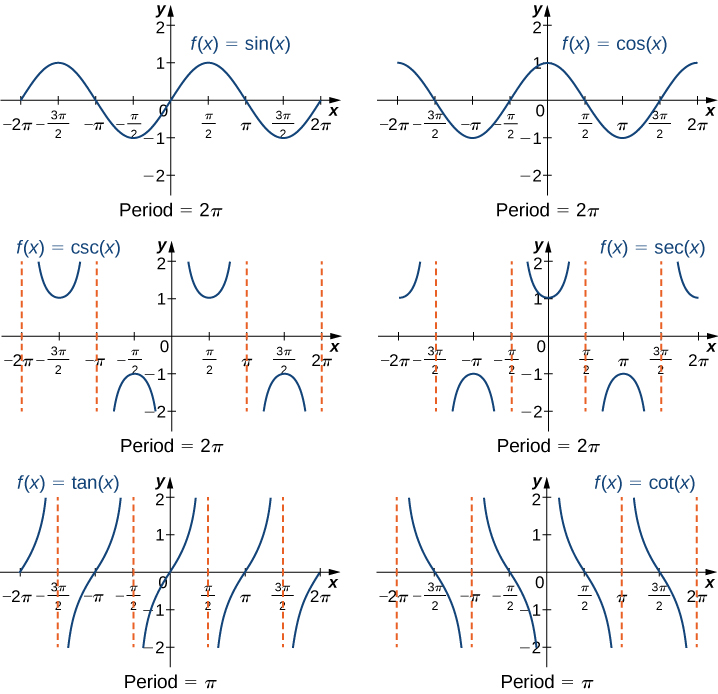
In trigonometry, the Trigonometric Functions Graph can prove to be of utmost convenience to all users. You can typically use these maps to understand each function of trigonometry.
- Integration Formula
- Formula of Trigonometry
- Trigonometric Ratios
- Trigonometric functions with Formulas
- What are Trigonometric derivatives
- Heights and distance
- Trigonometry formula Involving Sum Difference Product Identities
- Trig Identities
- Pythagorean Theorem
- Differentiation Formula
- Basic Trig Identities
Here in our article, we shall make our thorough discussion on the various graphs of trigonometric functions. You will be able to learn and drawing these maps on your own and for your personal usages.
Trigonometric Functions Graph
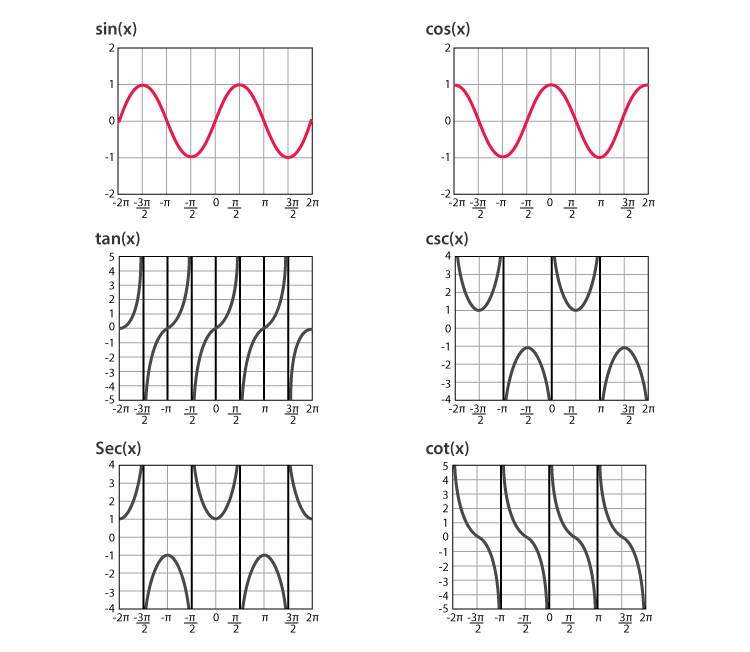
Trigonometric functions are the foundation of the whole trigonometry since it roams around only these functions. If you start studying trigonometry then functions will be the very first thing that you will come across in this domain of mathematics.
The main usage of trigonometric functions lies in the measurement of the triangles. These functions are extremely useful there to figure out the overall or the missing area of the triangle. So, there are basically six trigonometric functions that come into play while solving the various trigonometric problems.
For instance, with the trigonometric functions, you can measure the overall area of the triangles. In a similar manner, you can witness the direct application of the functions in those areas that include the fundamentals of geometry. It includes science, engineering, mechanism, navigation, etc.
Graphs of Trigonometric Functions
Well, the graph is probably the most potent tool to understand trigonometric functions and their applications. The graph helps in understanding how the trigonometric functions work with each other. You can witness and draw the separate or individual graph for each and all trigonometric functions as per your requirement. In this way, you can determine the value of each transaction function separately or collectively.
For instance, you can draw the graph for sine, cosine, and tangent functions together. You will need to have the minimum and maximum value of period, amplitude, phase. Upon drawing the map with these functions you can use it in several domains such as science & engineering etc.
So, basically, in a similar manner, you can draw the graph of other trigonometric functions separately or collectively. All these graphs have their own relevance across the various domains. The values of amplitude, period and phase are absolutely necessary in order to draw the graph of functions. You can check the several graphs of trigonometric functions in our article for your ultimate understanding. These graphs will definitely help you both in your academics and practical domains of life.