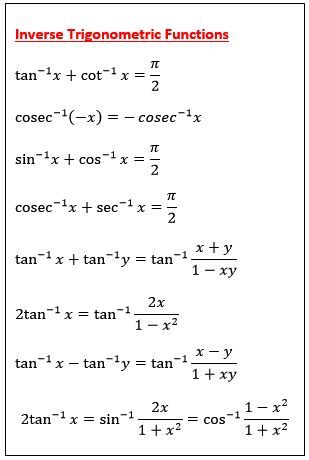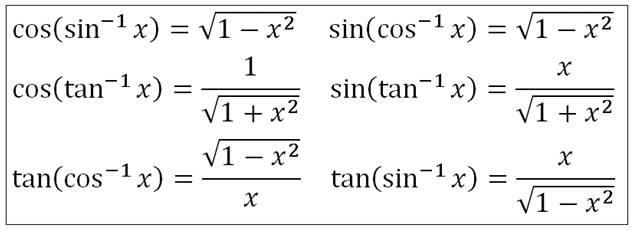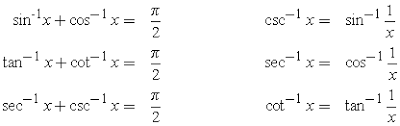The trigonometry inverse formula is one of the least talked about concepts of trigonometry. However, this formula is very significant in solving some complex problems in trigonometry. Here in the article, we are basically going to make our discussion on the trigonometry inverse formula for all our guests and readers.
- Integration Formula
- Formula of Trigonometry
- Trigonometric Ratios
- Trigonometric functions with Formulas
- What are Trigonometric derivatives
- Heights and distance
- Trigonometry formula Involving Sum Difference Product Identities
- Trig Identities
- Pythagorean Theorem
- Differentiation Formula
- Basic Trig Identities

Trigonometry is based on various types of formulas and the trigonometry inverse formula is one of them. You can use the formula across the numbers of usages to get the required results or values with the inverse trigonometry formula.
Trigonometry Inverse Formula
Well, in trigonometry the inverse trigonometry formula is also known as the arcus or cyclometric functions. The formula is actually based on the inverse functions of sine, cosine, tangent, secant, cosecant, and cotangent. The trigonometry inverse formula is useful in determining the angles of the given triangle.
You can easily witness the application of trigonometry inverse formula in the domain such as science, navigation, engineering, etc. So, you can use the reverse formula to solve the various trigonometric functions. You can also memorize these inverse trigonometry formulas for your reference. We urge you to have a regular practice of these formulas to get better learnings.
Trigonometry is the branch of mathematics that is highly useful in determining the area of a right-angle triangle. It’s basically the part of geometry and you will normally begin to read it in senior secondary high school. Trigonometry comes into play when we basically talk about the relationship between the triangle and the sides within the right triangle.
Inverse Trigonometry Formula List
Trigonometry uses a number of formulas to resolve the various types of problems based on the given question. The trigonometry inverse formula is one of those formulas that have the specific solution for the most specific problem. So at the end of the article, we urge our readers to practice the trigonometry inverse formula for their purpose. It will definitely prove to be very handy in the domain of trigonometry questions.