Limit Calculus – In the world of mathematics especially in calculus, the concept of limits plays an essential role. Limits are fundamental to understanding the behavior of functions and solving complex mathematical problems. In this article, we will delve into the world of limits, exploring what they are, why they matter, and how to work with them.
Limit Calculus
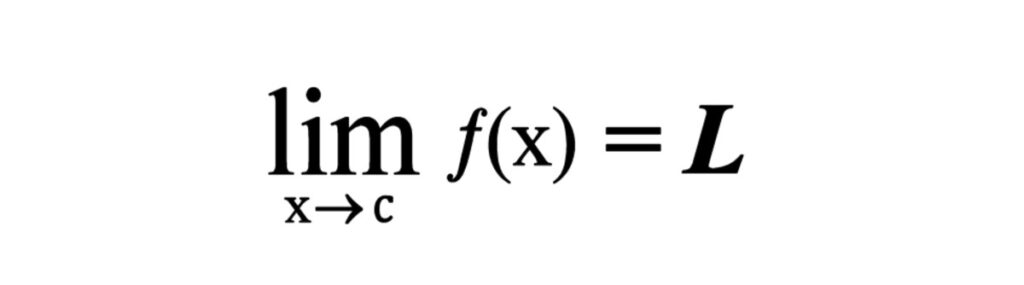
Whether you’re a student dealing with calculus or just curious about this mathematical concept, we’ll break it down in simple terms.
Definition of Limit Calculus
In calculus, a limit refers to the value a function approaches as it gets closer and closer to a specific point. This point is typically denoted as ‘c.’ We denote the limit of a function ‘f(x)’ as ‘L’ and write it as:
limx →c f(x) = L
We say that the limit of ‘f(x)’ as ‘x’ approaches ‘c’ is ‘L’ if, for every positive number ‘ε’ (epsilon), there exists a positive number ‘δ’ (delta) such that:
|f(x) – L| < ε whenever 0 < |x – c| < δ
Understanding limits is like having a key to unlock the secrets of calculus. It forms the foundation for various concepts within calculus, such as continuity, derivatives, and integrals. Limits help us analyze the behavior of functions, enabling us to tackle complex mathematical problems with ease.
Evaluating Limits Algebraically
Basic Algebraic Techniques for Evaluating Limits
Algebraic techniques are powerful ways for evaluating limits. Some essential methods include factoring, simplifying, and expanding expressions to make them responsive to limit evaluation.
Applying Limit Laws to Simplify Complex Expressions
Limit laws, such as the limit sum rule and limit product rule, allow us to simplify limits by breaking them down into manageable parts. These rules make evaluating the limits of complex functions more straightforward.
Solving Indeterminate Forms Using Algebraic Manipulation
Indeterminate forms like 0/0 or ∞/∞ often arise when evaluating limits. Algebraic manipulation techniques can help us resolve these indeterminate forms and find the actual limit.
Techniques for Evaluating Limit Calculus
Direct Substitution Method
The direct substitution method is the simplest way to evaluate limits. It involves substituting the value ‘c’ directly into the function ‘f(x)’ and calculating the limit.
Factoring and Canceling Techniques
Factoring and canceling techniques come in handy when dealing with rational functions. We can simplify the expression by factoring and canceling common factors to make limit evaluation easier.
Rationalizing Techniques
Rationalizing the numerator or denominator can help simplify expressions involving radicals, making them more manageable when evaluating limits.
L’Hôpital’s Rule for Evaluating Limits of Indeterminate Forms
When you encounter indeterminate forms like 0/0 or ∞/∞ that resist simplification, L’Hôpital’s rule provides an elegant solution. It allows us to differentiate the numerator and denominator separately, potentially resolving the limit.
A limit finder is a handy tool for evaluating limits according to the above methods with steps to ease up manual calculations
Examples For finding Limit Calculus
Example 1:
If f(x) = 2x + 1. What happens to ‘f(x)’ as ‘x’ approaches 3?
Solution:
We can calculate the limit as follows:
Step 1: Write the function with the limit notation.
limx →3 (2x + 1)
Step 2: Calculation
Replace x by 3
= 2(3) + 1
= 7
So, the limit of ‘f(x)’ as ‘x’ approaches 3 is 7.
Example 2:
g(x) = (x2 – 1) / (x – 1). As ‘x’ approaches to 1.
Solution:
Step 1: Write the function with the limit notation.
limx →1 [(x2 – 1) / (x – 1)]
If we apply a limit on the function; we will get a 0/0 form in the answer.
Step 2: Factorization
limx →1 [(x2 – 1) / (x – 1)]
Making the factors of x2 – 1
x2 – 1 = (x + 1) (x – 1)
Step 3: Calculation
limx →1 {(x + 1) (x – 1) / (x – 1)}
= limx →1 (x + 1)
Plugging in the limit
limx →1 (x + 1) = 1 + 1
limx →1 (x + 1) = 2
Applications of Limits
Determining Continuity and Differentiability of Functions
Limits help us determine whether a function is continuous or differentiable at a specific point. A continuous function has no jumps or holes, while differentiability indicates the smoothness of a function.
Finding the Slope of a Curve at a Specific Point
By evaluating limits, we can find the slope of a curve at a particular point. This is crucial for understanding the behavior of functions in calculus.
Calculating Instantaneous Rates of Change
Limits enable us to calculate instantaneous rates of change, which are essential for various real-world applications, such as physics and economics.
Understanding the Behavior of Functions Near Certain Points
Limits provide insights into how functions behave as we approach specific points. This information is invaluable for analyzing functions and solving complex problems.
Takeaway
Limits are not just a mathematical concept to memorize; they are the cornerstone of calculus. They open doors to understanding the behavior of functions, solving intricate problems, and making sense of the world through mathematics.
By understanding the basics of limits, their formal definition, and various evaluation techniques, you are well prepared to embark on your journey through the fascinating realm of calculus.
Hope you like this:


