A Trig Pie Chart is a visual representation of the six basic trigonometric functions: sine, cosine, tangent, cosecant, secant, and cotangent. These functions are used to describe the relationships between the angles and sides of a right triangle and are essential in many fields, including physics, engineering, and mathematics.
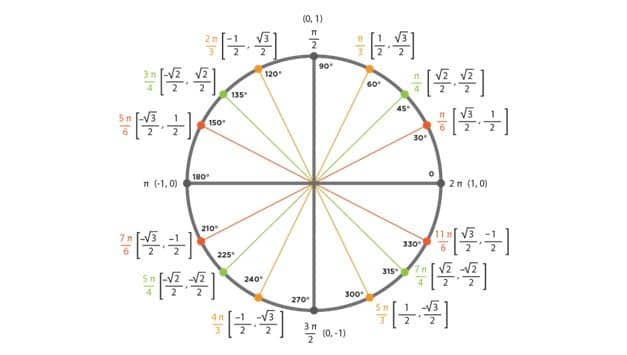
Trig Pie Chart – Function Relationship
A pie chart is a useful tool for remembering the relationships between these functions and understanding their values.
Each of the six trigonometry functions is represented by a sector in the pie chart, with the size of the sector indicating the value of the function. The angles of the triangle are placed at the center of the chart and are labeled with the Greek letters alpha (α), beta (β), and gamma (γ). The sides of the triangle are labeled with the letters adjacent (a), opposite (o), and hypotenuse (h).
Starting with sine, the sine of an angle is represented by the ratio of the opposite side to the hypotenuse. In other words, sin(α) = o/h. The sector of the pie chart representing sine is colored in red and is proportional to the value of sin(α). For example, if the angle is 30 degrees, the sine sector would take up 30% of the pie chart, as sin(30) = 0.5.
Next, the cosine function is represented by the ratio of the adjacent side to the hypotenuse. In other words, cos(α) = a/h. The sector of the pie chart representing cosine is colored in blue and is proportional to the value of cos(α). For example, if the angle is 60 degrees, the cosine sector would take up 60% of the pie chart, as cos(60) = 0.5.
The tangent function is represented by the ratio of the opposite side to the adjacent side. In other words, tan(α) = o/a. The sector of the pie chart representing tangent is colored in green and is proportional to the value of tan(α). For example, if the angle is 45 degrees, the tangent sector would take up 45% of the pie chart, as tan(45) = 1.
The cosecant function is represented by the reciprocal of the sine function. In other words, csc(α) = 1/sin(α). The sector of the pie chart representing cosecant is colored in purple and is proportional to the value of csc(α). For example, if the angle is 30 degrees, the cosecant sector would take up 2% of the pie chart, as csc(30) = 2.
The secant function is represented by the reciprocal of the cosine function. In other words, sec(α) = 1/cos(α). The sector of the pie chart representing secant is colored in orange and is proportional to the value of sec(α). For example, if the angle is 60 degrees, the secant sector would take up 2% of the pie chart, as sec(60) = 2.
Finally, the cotangent function is represented by the reciprocal of the tangent function. In other words, cot(α) = 1/tan(α). The sector of the pie chart representing cotangent is colored in yellow and is proportional to the value of cot(α). For example, if the angle is 45 degrees, the cotangent sector would take up 1% of the pie chart, as cot(45) = 1.

