Ready to discover the fundamental building blocks of Trigonometry? Trigonometry Ratios can help you do just that! Join us and learn about sine, cosine, and tangent ratios, their relationship with angles, and how to calculate them. Don’t miss out on this opportunity to enhance your mathematical skills!
Trigonometry Ratios
The links between triangles’ sides and angles studied in the mathematic discipline known as trigonometry. The trigonometric ratios ratios of the sides of a right triangle. That used to calculate the lengths of the sides and angles of a triangle.
These ratios the sine, cosine, tangent and cosine ratios.
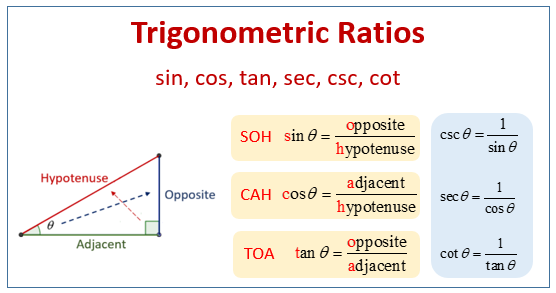
- The sine ratio (sin) is the ratio of the length of the side opposite the angle to the length of the hypotenuse. It is used to find the length of the side opposite a given angle in a right triangle.
- The cosine ratio (cos) is the ratio of the length of the adjacent side to the length of the hypotenuse. It is used to find the length of the side adjacent to a given angle in a right triangle.
- The tangent ratio (tan) is the ratio of the length of the opposite side to the length of the adjacent side. It is used to find the length of the side opposite or adjacent to a given angle in a right triangle.
Trigonometry Ratios Formulas
The following six trigonometric ratios formula: –
- Sine (sin) ratio: sinθ = Opposite side / Hypotenuse
- Cosine (cos) ratio: cosθ = Adjacent side / Hypotenuse
- Tangent (tan) ratio: tanθ = Opposite side / Adjacent side
- Cosecant (csc) ratio: cscθ = 1 / sinθ (reciprocal of sine)
- Secant (sec) ratio: secθ = 1 / cosθ (reciprocal of cosine)
- Cotangent (cot) ratio: cotθ = 1 / tanθ (reciprocal of tangent)
These ratios represent the relationships between the sides of a right triangle and used to calculate the trigonometric values of angles. The numerator of each ratio corresponds to a specific side length, while the denominator represents the hypotenuse or adjacent side.
It’s important to note that these formulas hold true only for right triangles. For other types of triangles or non-right angles, trigonometric functions are calculated differently using advanced concepts like the unit circle or trigonometric identities. Check out other related posts to trigonometry:- Differentiation Formula for Trigonometric Functions
Trig Ratios
These ratios used to solve many mathematical problems, including finding missing sides and angles in a triangle, finding the length of a side of a triangle given the length of another side and an angle, and finding the angle of a triangle given the length of two sides.
In addition to the above ratios, two more ratios, cosecant and secant, used in trigonometry. The cosecant ratio (csc) is the reciprocal of the sine ratio, while the secant ratio (sec) is the reciprocal of the cosine ratio. These ratios used in advanced trigonometry problems.
In conclusion, trigonometric ratios an essential part of trigonometry. And widely used in mathematics, engineering, physics, and many other fields. Understanding and using these ratios is crucial for solving many mathematical problems. It making sense of the relationships between the sides and angles of triangles.
How to Find Trigonometric Ratios
Finding trigonometric ratios involves using the ratios of the sides of a right triangle. The three primary trigonometric ratios- sine (sin), cosine (cos), and tangent (tan). Here’s how you can find these ratios:
-
Identify the right triangle: Make sure you have a triangle with one angle measuring 90 degrees (a right angle).
-
Label the sides: In the right triangle, identify the three sides relative to the angle you working with. The two shorter sides typically labeled as the adjacent side (denoted as “adj”) and the opposite side (denoted as “opp”). The longest side, which is the hypotenuse (denoted as “hyp”), is always opposite the right angle.
-
Determine the trigonometric ratio:
- Sine (sin): To find the sine ratio, divide the length of the opposite side by the length of the hypotenuse. sinθ = opp/hyp.
- Cosine (cos): To find the cosine ratio, divide the length of the adjacent side by the length of the hypotenuse. cosθ = adj/hyp.
- Tangent (tan): To find the tangent ratio, divide the length of the opposite side by the length of the adjacent side. tanθ = opp/adj.
-
Use a calculator: If you need to find the trigonometric ratios of angles other than the commonly used angles (30°, 45°, and 60°), you can use a scientific calculator with trigonometric functions. Simply enter the angle in degrees and press the appropriate trigonometric button (sin, cos, or tan) to get the ratio.
Remember, the trigonometric ratios vary based on the angle you working with. By understanding the relationships between the sides of a right triangle and using the appropriate ratios, you can find the trigonometric ratios for any given angle.