The Derivatives of Arc Trig Functions is an important topic in calculus. Arc trigonometric functions are the inverse functions of the usual trigonometry functions (sine, cosine, tangent, etc.). They provide the angle of a triangle given the ratio of its sides.
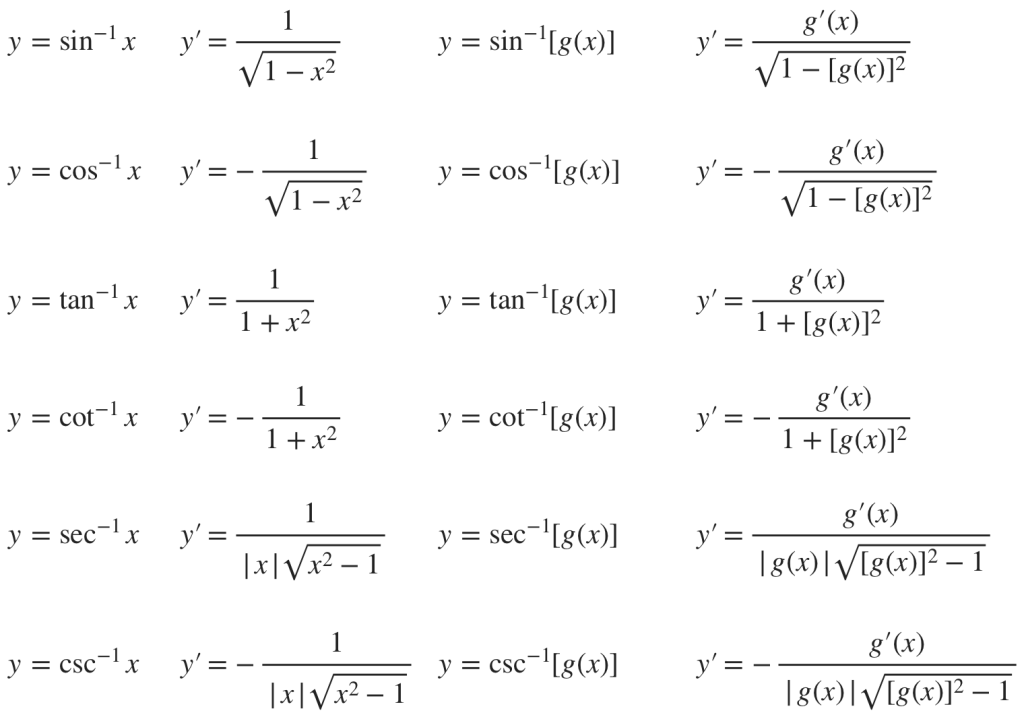
Derivatives of Arc Trig Functions
In order to find the derivative of an arc trigonometric function, we first need to establish the relationship between the function and its inverse. Consider the function y = sin(x). Its inverse function, denoted as y = sin^(-1)(x), is defined such that for any value of x, sin(sin^(-1)(x)) = x. In other words, sin^(-1)(x) gives us the angle whose sine is x.
These are some example for arc trig functions, Now, suppose we have a differentiable function y = sin^(-1)(x). To find its derivative, we use the inverse function theorem, which states that if f is a differentiable function with a non-zero derivative at a point x, then its inverse function g also has a derivative at g(x) and it is given by:
dg/dx = 1/df/dx
where f(x) = sin^(-1)(x) and g(x) = sin(x).
Taking the derivative of both sides of the equation sin(sin^(-1)(x)) = x with respect to x, we get:
cos(sin^(-1)(x)) * d(sin^(-1)(x))/dx = 1
Since cos(sin^(-1)(x)) is non-zero, we can divide both sides of the equation by cos(sin^(-1)(x)) to get:
d(sin^(-1)(x))/dx = 1/cos(sin^(-1)(x))
Therefore, the derivative of the inverse sine function, sin^(-1)(x), is equal to 1/cos(sin^(-1)(x)).
Similarly, the derivative of the inverse cosine function, cos^(-1)(x), is given by:
d(cos^(-1)(x))/dx = -1/sqrt(1 – x^2)
and the derivative of the inverse tangent function, tan^(-1)(x), is given by:
d(tan^(-1)(x))/dx = 1/(1 + x^2)
It is important to note that the domain of the arc trigonometric functions is limited to specific intervals, based on the range of the corresponding trigonometric functions. For example, the range of sine is [-1, 1], and the domain of its inverse function sin^(-1)(x) is also [-1, 1].
The derivative of an arc trigonometric function.

