How To Find Height In Trigonometry ,the height of an object can be found using trigonometry by relating the height to the angles and lengths of the sides of a right triangle formed between the object, the observer, and the ground. If the angle of elevation or depression of the object is known, the height can be calculated using trigonometric functions such as sine, cosine, or tangent.
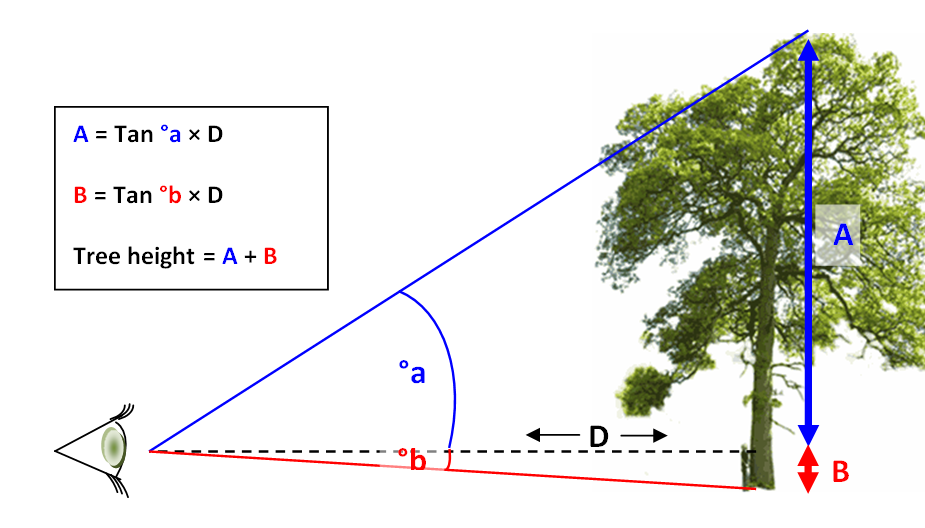
How To Find Height In Trigonometry – Examples
- Example 01:
Given an observer, the ground, and a tower, and the angle of elevation of the top of the tower from the observer is θ, and the distance between the observer and the tower is d. The height of the tower, h, can be found using the tangent function:
h = d * tan(θ)
The same method can be applied using sine or cosine functions. - Example 02:
Let’s consider a right triangle with sides a and b and height h.
Using the Pythagorean theorem, we can write:
a^2 + b^2 = h^2
Now, if we know the angles in the triangle, we can use trigonometry to find the height. For example, if we know the angle θ, we can use the sine function to find h:
h = b * sin(θ)
Or, if we know the angle Φ, we can use the cosine function to find h:
h = a * cos(Φ)
Thus, by knowing either the angles or the sides, we can use trigonometry to find the height of a triangle.
How To Find Height In Trig – With Theorem or Ratios
To find the height in trigonometry, you need to use the Pythagorean theorem or the trigonometric ratios.
- Pythagorean Theorem:
The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides. To find the height, we can use the theorem as follows:
a^2 + b^2 = c^2
Where a and b are the lengths of the two sides, and c is the length of the hypotenuse. - Trigonometric Ratios:
We can use the trigonometric ratios such as sine, cosine, or tangent to find the height. For example, if we know the angle between the height and the base and the length of the base, we can use the sine function to find the height.
height = base * sin(angle)
By using either of these methods, we can find the height in a triangle.
In conclusion, Trigonometry has a wide range of applications in fields such as engineering, physics, and astronomy, and is used to solve problems related to height and distance, wave behavior, and navigation.

