Take your Trigonometry expertise to the next level with Double Angle Trig Identities! These powerful identities provide a shortcut to calculating angles and help simplify complex equations. Join us and unlock the full potential of Trigonometry with ease.
Double Angle Trig Identities
Double-angle trigonometric identities are mathematical expressions that define the relationship between the trigonometric functions of double the size of an angle.
In trigonometry, double angle identities relate the values of trigonometric functions of angles that are twice as large as a given angle. These identities can be derived from the sum and difference identities for sine and cosine.
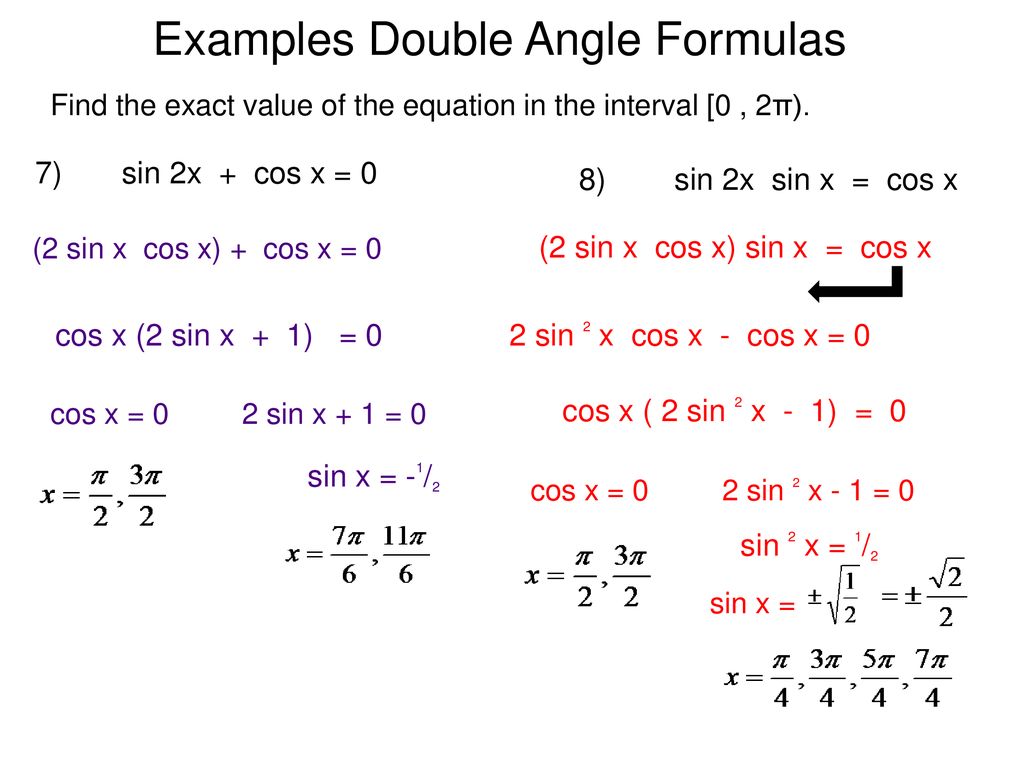
These identities come in handy when solving complex trigonometric problems, especially those that involve triangles and circles. Here are a few of the most important double-angle identities:
Sine of double angle formula:
sin(2θ) = 2sinθcosθ
This identity relates the sine of double an angle to the product of the sine and cosine of that angle. It is commonly used to simplify complex trigonometric expressions and to find the sine of an angle given the sine and cosine of half that angle.
Cosine of double angle formula:
cos(2θ) = cos^2θ – sin^2θ
This identity defines the relationship between the cosine of double an angle and the square of the sine and cosine of that angle. It is commonly used to find the cosine of an angle given the sine. Cosine of half that angle and to simplify complex trigonometric expressions.
Double Angle Trigonometry Identities
Tangent of double angle formula:
tan(2θ) = 2tanθ / 1 – tan^2θ
This identity relates the tangent of double an angle to the tangent of that angle. It is commonly used to find the tangent of an angle given the tangent of half that angle and to simplify complex trigonometric expressions.
Secant of double angle formula:
sec(2θ) = 1 / [2cosθ * (1 + cos^2θ)]
This identity defines the relationship between the secant of double an angle and the cosine of that angle. It is commonly used to find the secant of an angle given the cosine of half that angle and to simplify complex trigonometric expressions.
Cosecant of double angle formula:
csc(2θ) = 1 / [2sinθ * (1 + cos^2θ)]
This identity relates the cosecant of double an angle to the sine and cosine of that angle. It is commonly used to find the cosecant of an angle given the sine and cosine of half that angle and to simplify complex trigonometric expressions.
Cotangent of double angle formula:
cot(2θ) = (1 – tan^2θ) / 2tanθ
This identity defines the relationship between the cotangent of double an angle and the tangent of that angle. It is commonly used to find the cotangent of an angle given the tangent of half that angle and to simplify complex trigonometric expressions.
Trig Double Angle Identities
It is important to note that double-angle identities are derived from the Pythagorean identity. That states that the square of the sine and cosine of an angle is equal to one. This identity forms the basis of many trigonometric expressions, including double-angle identities.
Double-angle identities can be used to solve a variety of problems in mathematics, physics, and engineering. For example, they can be used to find the length of the sides of a triangle given the angles, to calculate the area of a circle, and to solve problems involving waves and oscillations.
In conclusion, double-angle trigonometric identities are useful mathematical expressions that define the relationship between the trigonometric functions of double the size of an angle. Understanding these identities and how to use them is essential for anyone studying trigonometry, geometry, physics, or engineering.

