Ready to simplify complex Trigonometry equations? Quotient Trig Identities can help you do just that! Join us and discover powerful techniques for expressing trig functions as fractions. Enhance your skills and unlock new possibilities in the world of Trigonometry!
Quotient Trig Identities
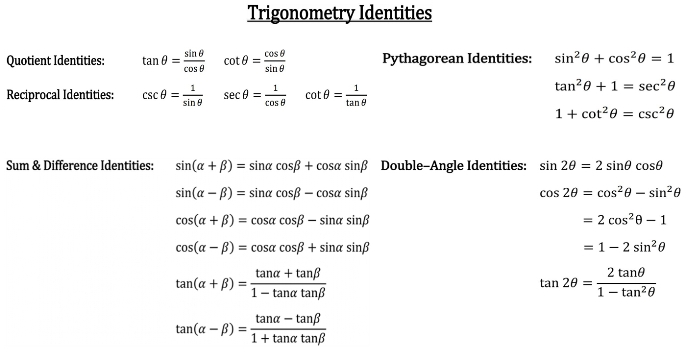
Quotient Trig Identities are relationships between ratios of two trigonometric functions that are used to simplify and evaluate expressions involving these functions. These identities are widely used in solving problems related to triangles, circles, and other geometric figures.
Quotient Trigonometry Identities
In this article, we will discuss some of the most commonly used quotient trigonometry identities and their applications.
- The tangent identity: The tangent of an angle is defined as the ratio of the sine and cosine of the angle. Mathematically, it can be expressed as tan(θ) = sin(θ) / cos(θ). This identity is particularly useful in solving triangles, where the sides and angles can be related to each other using the tangent function. For example, if we know the length of two sides of a right triangle, we can use the tangent identity to find the third side.
- The cotangent identity: The cotangent of an angle is defined as the reciprocal of the tangent of the angle. Mathematically, it can be expressed as cot(θ) = 1 / tan(θ). This identity is useful in solving triangles where the side lengths are known and the angles need to be found.
- The secant identity: The secant of an angle is defined as the reciprocal of the cosine of the angle. Mathematically, it can be expressed as sec(θ) = 1 / cos(θ). This identity is useful in finding the length of the hypotenuse of a right triangle given the lengths of the other two sides.
- The cosecant identity: The cosecant of an angle is defined as the reciprocal of the sine of the angle. Mathematically, it can be expressed as csc(θ) = 1 / sin(θ). This identity is useful in finding the length of one of the sides of a right triangle given the length of the hypotenuse and one of the other sides.
Quotient Trig Identities – Trigonometry Identities
In addition to these basic identities, there are several other quotient trigonometric identities that are useful in solving more complex problems. For example, the double angle identities, which allow us to find the sine and cosine of twice an angle given the sine and cosine of the original angle.
One of the applications of these identities is in finding the length of sides of a triangle when the angles and one or more side lengths are known. This can be done using the tangent, cotangent, secant, and cosecant identities. For example, if we know two side lengths of a right triangle and the measure of one of its angles, we can use the tangent identity to find the third side length.
Similarly, if we know the length of the hypotenuse and one of the other sides, we can use the cosecant identity to find the length of the other side.
Another application of these identities is in solving problems related to circles. For example, we can use the secant and cosecant identities to find the length of a chord in a circle given the measure of the central angle subtended by the chord.
In addition to these applications, the quotient trigonometric identities are also used in solving problems related to wave motion and oscillations, including simple harmonic motion. In these applications, the sine and cosine functions are used to describe the motion of a particle or wave over time. The identities can be used to simplify expressions involving these functions, making it easier to analyze the motion and understand its properties.

