If you’ve ever wondered how to handle angles that are not so straightforward, you’ve come to the right place. Half Angle Trig Identities are powerful tools that help us deal with these tricky situations. In this article, we’ll explore the essential half-angle trig identities formulas and provide clear examples to illustrate their practical applications. By the end of this guide, you’ll have a solid understanding of how to work with half angles in trigonometry and expand your problem-solving skills in this fascinating branch of mathematics.
Half Angle Trig Identities
Half angle trig identities, a set of fundamental mathematical relationships used in trigonometry to express trigonometric functions of an angle in terms of functions of half that angle. These identities particularly useful when dealing with complex trigonometric problems, simplifying expressions, and solving equations. The half angle identities derived from the double angle identities and play a crucial role in various branches of mathematics and engineering.
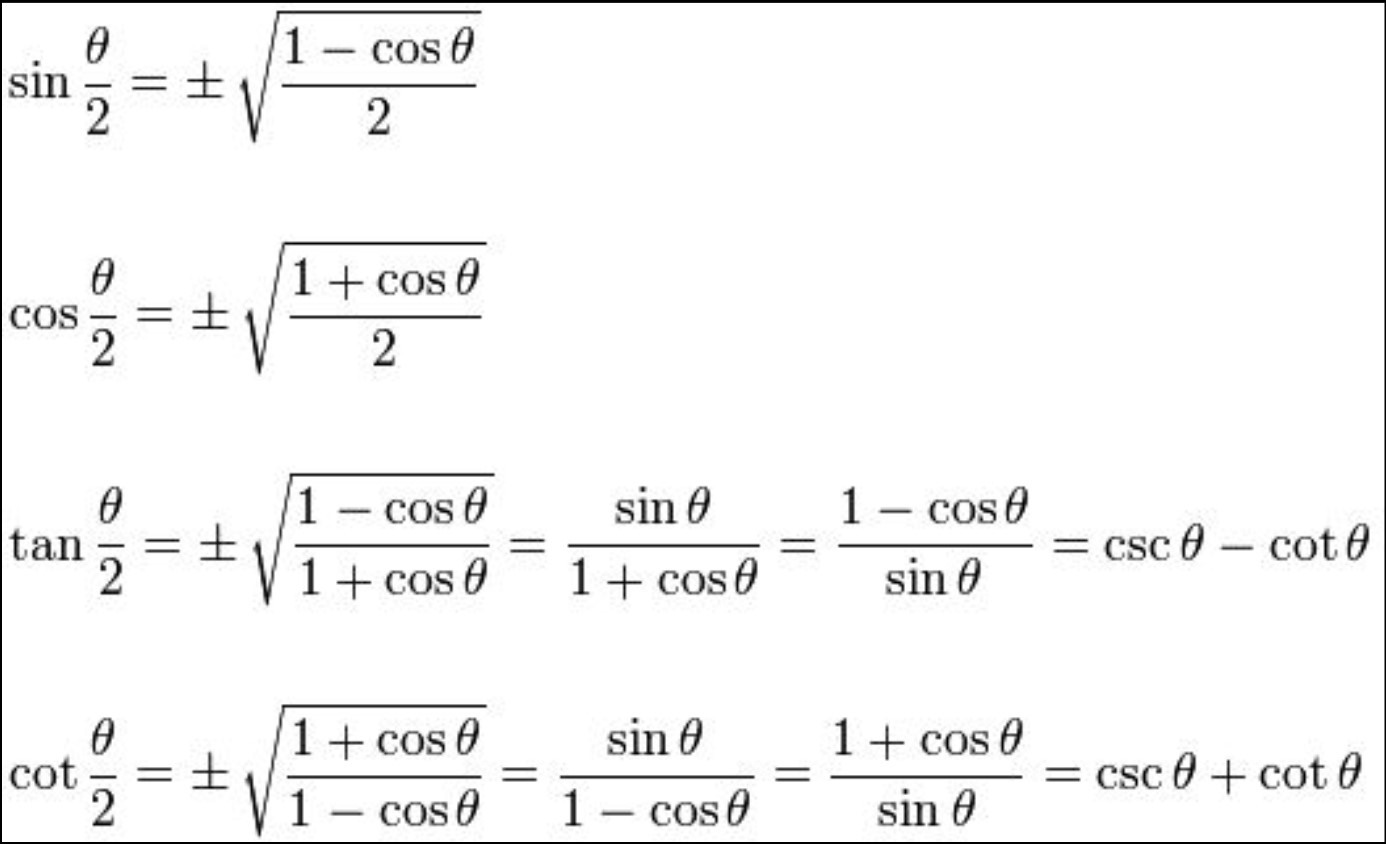
The most commonly used half angle identities are:
- Sine Half Angle Identity: sin(x/2) = ±√[(1 – cos(x))/2]
- Cosine Half Angle Identity: cos(x/2) = ±√[(1 + cos(x))/2]
- Tangent Half Angle Identity: tan(x/2) = ±√[(1 – cos(x))/(1 + cos(x))]
Where x is the angle in question. The ± sign is used to indicate that the identity’s value depends on the quadrant in which the angle lies.
These identities can employed in a wide range of applications, such as in calculus, physics, engineering, and geometry. They especially valuable when integrating trigonometric functions, simplifying expressions, and solving trigonometric equations. By skillfully utilizing the half angle trig identities, mathematicians and scientists able to tackle complex problems with greater ease and efficiency.
Trigonometry Half Angle Formulas and Examples
Trigonometry half angle formulas play a significant role in solving trigonometric problems that involve angles halved from their original values. These formulas provide a means to express sine, cosine, and tangent functions in terms of half of the original angle, simplifying calculations and manipulations in trigonometric equations.
Let’s take a look at some examples to illustrate the use of half angle formulas:
Example 1: Given that cos(x) = -3/5 and x is in the second quadrant, we want to find cos(x/2). Solution: Since x is in the second quadrant, cos(x/2) positive. Using the cosine half angle identity, we have: cos(x/2) = √[(1 + cos(x))/2] cos(x/2) = √[(1 – 3/5)/2] cos(x/2) = √[(2/5)/2] cos(x/2) = √(1/5) cos(x/2) = √5 / 5
Example 2: Given that tan(y) = 4/3 and y is in the fourth quadrant, we want to find tan(y/2). Solution: In the fourth quadrant, tan(y/2) positive. Using the tangent half angle identity, we have: tan(y/2) = √[(1 – cos(y))/(1 + cos(y))] tan(y/2) = √[(1 – 4/5)/(1 + 4/5)] tan(y/2) = √[(1/5)/(9/5)] tan(y/2) = √(1/9) tan(y/2) = 1/3
These examples demonstrate the application of half angle formulas in finding trigonometric values of angles effectively and efficiently.
Double‐Angle and Half‐Angle Identities
Double‐angle and half‐angle identities essential tools in trigonometry that establish relationships between trigonometric functions of angles when those angles either doubled or halved. These identities derived from the sum and difference identities, and they find extensive application in various mathematical and engineering fields.
The double‐angle identities are as follows:
- Double‐Angle Sine Identity: sin(2x) = 2 * sin(x) * cos(x)
- Double‐Angle Cosine Identity: cos(2x) = cos^2(x) – sin^2(x) = 2 * cos^2(x) – 1 = 1 – 2 * sin^2(x)
- Double‐Angle Tangent Identity: tan(2x) = (2 * tan(x)) / (1 – tan^2(x))
On the other hand, the half‐angle identities derived from the double‐angle identities and areexpressed as:
- Sine Half‐Angle Identity: sin(x/2) = ±√[(1 – cos(x))/2]
- Cosine Half‐Angle Identity: cos(x/2) = ±√[(1 + cos(x))/2]
- Tangent Half‐Angle Identity: tan(x/2) = ±√[(1 – cos(x))/(1 + cos(x))]
The ± sign in the half‐angle identities indicates that the value depends on the quadrant in which the angle lies, similar to the original half angle trig identities.
These double‐angle and half‐angle identities are instrumental in simplifying trigonometric expressions, solving trigonometric equations, and evaluating integrals. Engineers, physicists, and mathematicians frequently rely on these identities to solve complex problems involving trigonometric functions in various fields. Mastery of these identities is fundamental to advancing one’s understanding and proficiency in trigonometry.

