Cosine trigonometric identities, a crucial set of mathematical relationships used in trigonometry to express various trigonometric functions in terms of cosine and sine. These Cos Trig Identities play a fundamental role in simplifying complex trigonometric expressions and solving equations involving cosine and sine functions. By understanding these identities, mathematicians, engineers, and scientists gain a powerful toolkit to analyze and solve a wide range of problems in different fields.
Cos Trig Identities
Cosine trigonometric identities – fundamental equations that relate the cosine function to other trigonometric functions and angles. These identities play a crucial role in solving various mathematical problems and widely used in calculus, physics, engineering, and many other fields. One of the most well-known cosine identities is the Pythagorean identity, which states that the square of the cosine of an angle added to the square of the sine of the same angle equals one.
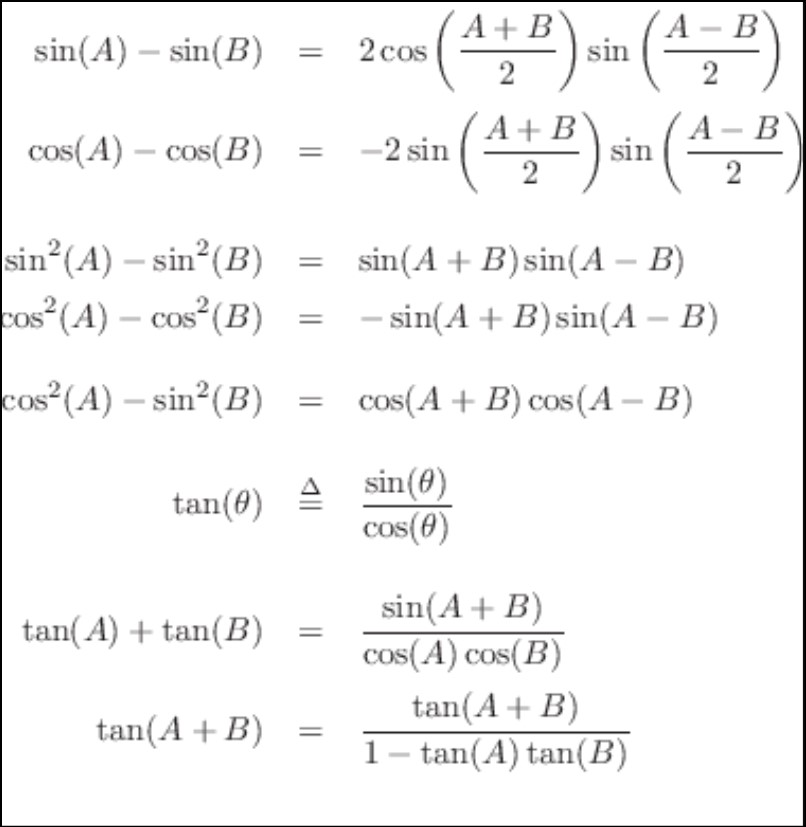
Mathematically, it can expressed as follows:
cos^2(theta) + sin^2(theta) = 1
Another essential identity is the double angle identity for cosine, which provides a way to express the cosine of twice an angle in terms of the cosine of the original angle. For any angle theta, the double angle identity is given by:
cos(2 * theta) = cos^2(theta) – sin^2(theta)
Cosine trig identities not limited to double angles; there also half-angle identities, product-to-sum identities, and sum-to-product identities involving the cosine function. These identities instrumental in simplifying complex trigonometric expressions, evaluating integrals, and solving trigonometric equations. They provide a powerful toolkit for mathematicians, scientists, and engineers to analyze and understand various phenomena that involve periodic behavior.
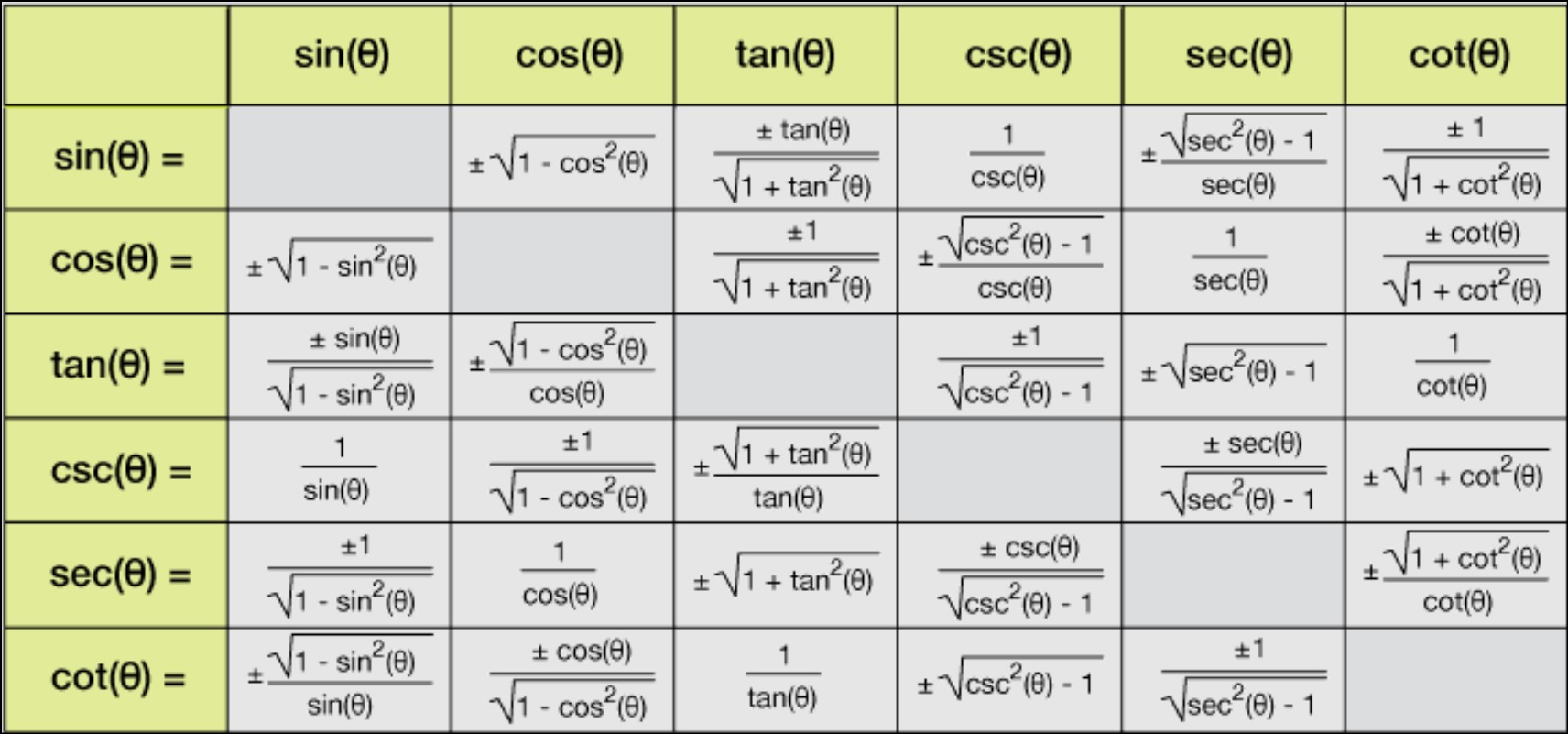
Trig Identities in Terms of Sin and Cos
Trigonometric identities essential tools for simplifying and manipulating trigonometric expressions. Many of these identities expressed in terms of both sine (sin) and cosine (cos) functions.
One such identity is the tangent (tan) identity, which defines the tangent of an angle theta as the ratio of sine to cosine:
tan(theta) = sin(theta) / cos(theta)
Similarly, the cotangent (cot) identity is the reciprocal of the tangent and is defined as the ratio of cosine to sine:
cot(theta) = cos(theta) / sin(theta)
Another notable example is the cosecant (csc) identity, which is the reciprocal of the sine function:
csc(theta) = 1 / sin(theta)
Similarly, the secant (sec) identity is the reciprocal of the cosine function:
sec(theta) = 1 / cos(theta)
These identities particularly useful when dealing with trigonometric expressions involving different trigonometric functions. They provide a means of converting between sine and cosine functions and allow mathematicians and scientists to express complex trigonometric expressions in simpler terms.
Cos Over Sin Identity
The cosine over sine identity is a fundamental trigonometric identity that relates the ratio of cosine to sine for a given angle.
For any angle theta, the identity is expressed as follows:
cot(theta) = cos(theta) / sin(theta)
This identity is a variation of the cotangent identity, where the cotangent of an angle the reciprocal of the tangent. By dividing the cosine of an angle by its corresponding sine, we obtain the cotangent, which represents the ratio of the adjacent side to the opposite side in a right triangle.
The cotangent identity finds applications in various fields, such as physics and engineering, where it used to analyze alternating current (AC) circuits, vibrations, and harmonic motion. In these contexts, the ratio of the cosine to the sine of an angle plays a crucial role in determining phase differences and amplitude relationships.
Furthermore, the cotangent identity can used to derive other trigonometric identities, such as the Pythagorean identity. By dividing both sides of the Pythagorean identity (cos^2(theta) + sin^2(theta) = 1) by sin^2(theta), we can arrive at the cotangent identity:
cot^2(theta) + 1 = csc^2(theta)
In summary, the cos over sin identity (cot(theta) = cos(theta) / sin(theta)) an essential trigonometric identity that appears in various mathematical and scientific contexts. Its applications range from solving right triangles to analyzing complex oscillatory systems, making it a valuable tool in understanding and solving real-world problems.