How to Find Angle In Trigonometry – [Angle Measures]

Unleash your ability to know How to Find Angle In Trigonometry with our expert guidance! Whether you’re a beginner or looking to enhance your skills, we’ll teach you how to calculate angles using a variety of techniques. Join us and master the art of Trigonometry!

How to Find Angle In Trigonometry

To find an angle in trigonometry, you typically use the inverse trigonometric functions. These functions denoted by “arc” or “inverse” prefixes and the inverse operations of the trigonometric functions.

The most commonly used inverse trigonometric functions are:

1. Arcsine (sin^(-1) or asin): Used to find the angle whose sine a given value. For example: If sinθ = 0.5, then θ = sin^(-1)(0.5) or asin(0.5).

2. Arccosine (cos^(-1) or acos): Used to find the angle whose cosine a given value. For example: If cosθ = 0.5, then θ = cos^(-1)(0.5) or acos(0.5).

3. Arctangent (tan^(-1) or atan): Used to find the angle whose tangent a given value. For example: If tanθ = 0.5, then θ = tan^(-1)(0.5) or atan(0.5).

These inverse trigonometric functions usually available on scientific calculators and programming languages. Here’s a step-by-step process to find an angle using these functions:

1. Identify the trigonometric function involved (sine, cosine, or tangent) and the given value.
2. Use the appropriate inverse trigonometric function (arcsine, arccosine, or arctangent) corresponding to the function identified in step 1.
3. Plug in the given value into the inverse trigonometric function.
4. Calculate the result, which will the angle in radians.
5. If you need the angle in degrees, convert the result from radians to degrees by multiplying by 180/π (180 divided by pi, where pi approximately 3.14159).

It’s important to note that inverse trigonometric functions typically multi-valued. To determine the appropriate angle, you need to consider the domain and range of the function and any additional information provided in the problem. Check out other posts:- Basics of Derivative Calculus

How To Find Angle Measures Using Trigonometry

Here the steps to find angle measures using trigonometry:

1. Identify the right triangle: Make sure you have a triangle with one angle that measures 90 degrees (a right angle). This essential for using trigonometry.

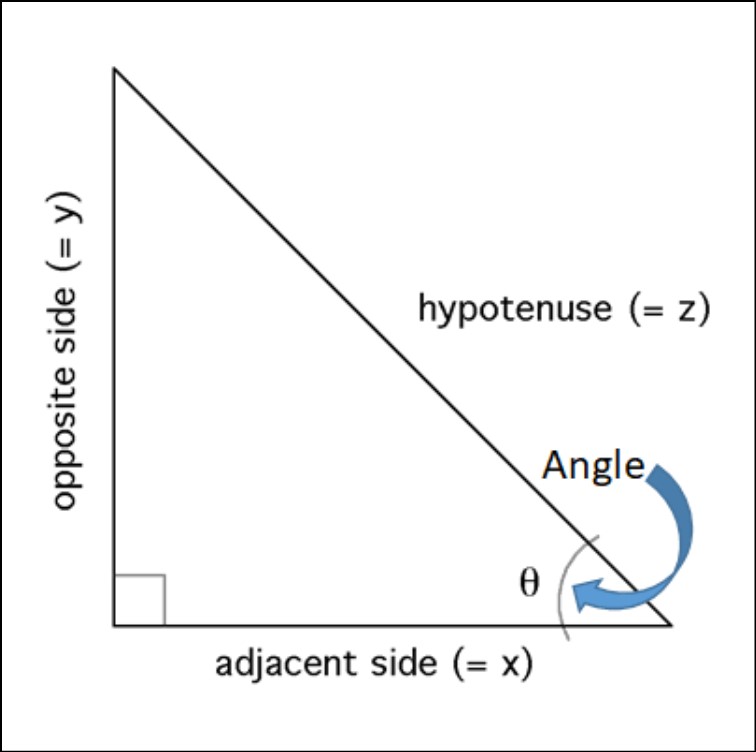
2. Label the sides: Identify the three sides of the triangle. The side opposite the right angle called the hypotenuse (labeled ‘h’), and the other two sides the adjacent side (labeled ‘a’) and the opposite side (labeled ‘o’).

3. Determine which angle you want to find: Identify the angle for which you want to determine the measure.

4. Choose the appropriate trigonometric function: Depending on the given information and the angle you want to find, select the appropriate trigonometric function: sine (sin), cosine (cos), or tangent (tan).

   • To find the sine of an angle: sin(angle) = opposite/hypotenuse (o/h).
   • To find the cosine of an angle: cos(angle) = adjacent/hypotenuse (a/h).
   • To find the tangent of an angle: tan(angle) = opposite/adjacent (o/a).

5. Rearrange the formula and solve for the angle: Rearrange the equation to isolate the angle you want to find.

   • To find the angle given the sine: angle = arcsin(opposite/hypotenuse).
   • To find the angle given the cosine: angle = arccos(adjacent/hypotenuse).
   • To find the angle given the tangent: angle = arctan(opposite/adjacent).

6. Use a scientific calculator or trigonometric tables: Use a scientific calculator or consult trigonometric tables to find the inverse trigonometric functions (arcsin, arccos, arctan). These functions will give you the angle in radians.

7. Convert the angle to degrees if necessary: If the angle required in degrees, multiply the radian measure by (180/π) to convert it.

How to Find Angle In Trigonometry -Step by Step

These ratios, known as sine (sin), cosine (cos), and tangent (tan), can used to find the measure of an angle given the lengths of the sides of a right triangle.

Here is a step-by-step guide to finding an angle in trigonometry:
• Identify a right triangle with known side lengths.
• Choose the ratio that relates the angle you want to find to the side lengths of the triangle.
• Use the Pythagorean theorem to find the lengths of the other sides if necessary.
• Use a trigonometry table or calculator to find the value of the ratio you chose.
• Use the inverse trigonometric function to find the measure of the angle.

Note: The measure of an angle in trigonometry always in radians. To convert to degrees, multiply the angle measure in radians by 180/π.

Trigonometry To Find Angles

To find an angle in a right triangle using trigonometry, you can use one of the following formulas:
• Sine (sin): sin(θ) = opposite/hypotenuse
• Cosine (cos): cos(θ) = adjacent/hypotenuse
• Tangent (tan): tan(θ) = opposite/adjacent
Where θ the angle, you trying to find, opposite the side opposite to the angle, adjacent the side adjacent to the angle and hypotenuse the longest side of the triangle (also known as the hypotenuse).

Once you have the value of one of the trigonometric ratios, you can use the inverse function (arc sin, arc cos, arctan) to find the measure of the angle.
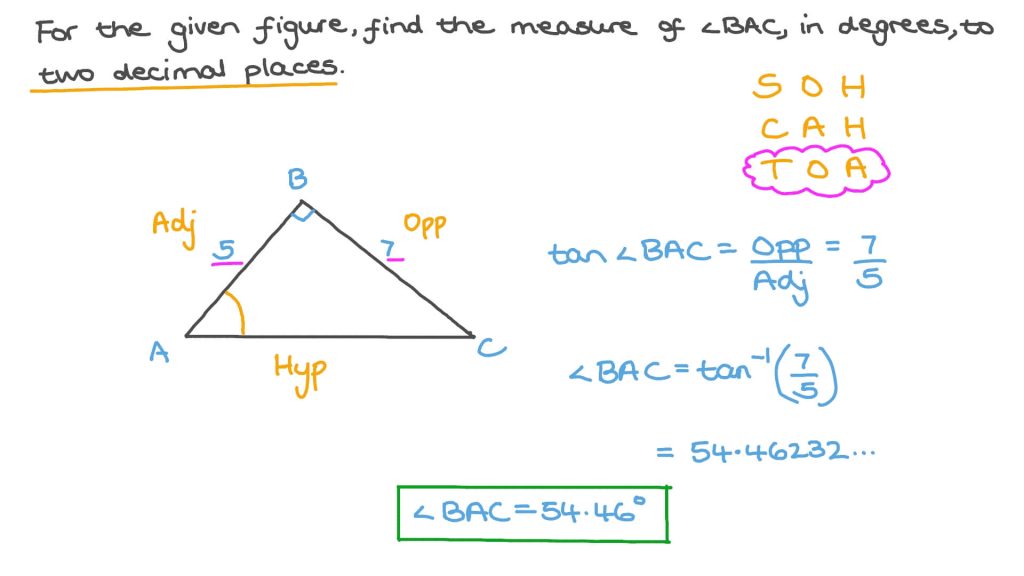
For example, if you have a right triangle with sides a=8 and b=15, and you want to find the measure of the angle opposite the side of length 8, you would use the formula:
tan(θ) = 8/15
Solving for θ using the inverse tangent function:
θ = arctan (8/15)

In conclusion, an angle can defined as a portion of a circle that created by two rays or lines with a common endpoint called the vertex. The measure of an angle usually expressed in degrees or radians. The size of an angle determines the shape and size of a triangle and can used to calculate the trigonometric functions such as sine, cosine, and tangent.