Reciprocal identities are fundamental concepts in trigonometry that play a crucial role in simplifying and manipulating trigonometric expressions. These identities involve the reciprocal functions of sine, cosine, and tangent, and they are essential tools for solving trigonometric equations, proving identities, and making calculations more manageable. In this comprehensive guide, we will delve into reciprocal identities in trigonometry, exploring their significance and providing clear examples to help you grasp their application and utility.
Reciprocal Identities Trigonometry
Reciprocal identities are an essential set of trigonometric relationships that highlight the interconnected nature of trigonometric functions. These identities involve the reciprocal values of sine, cosine, tangent, cosecant, secant, and cotangent functions. Understanding these identities is crucial for simplifying trigonometric expressions and solving various mathematical problems.
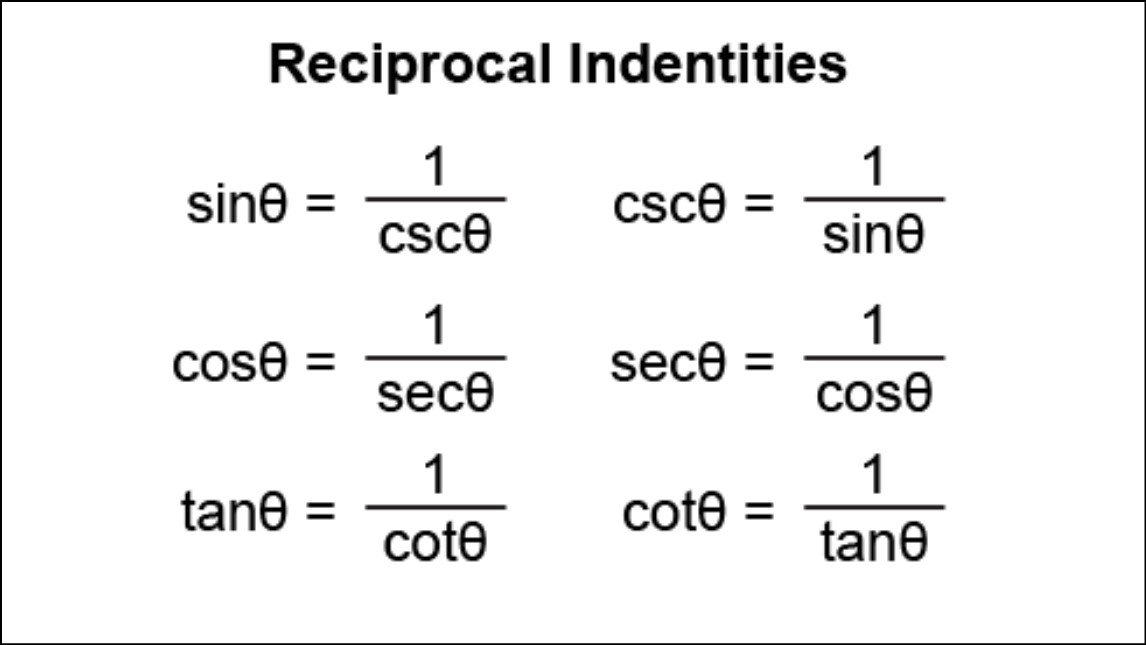
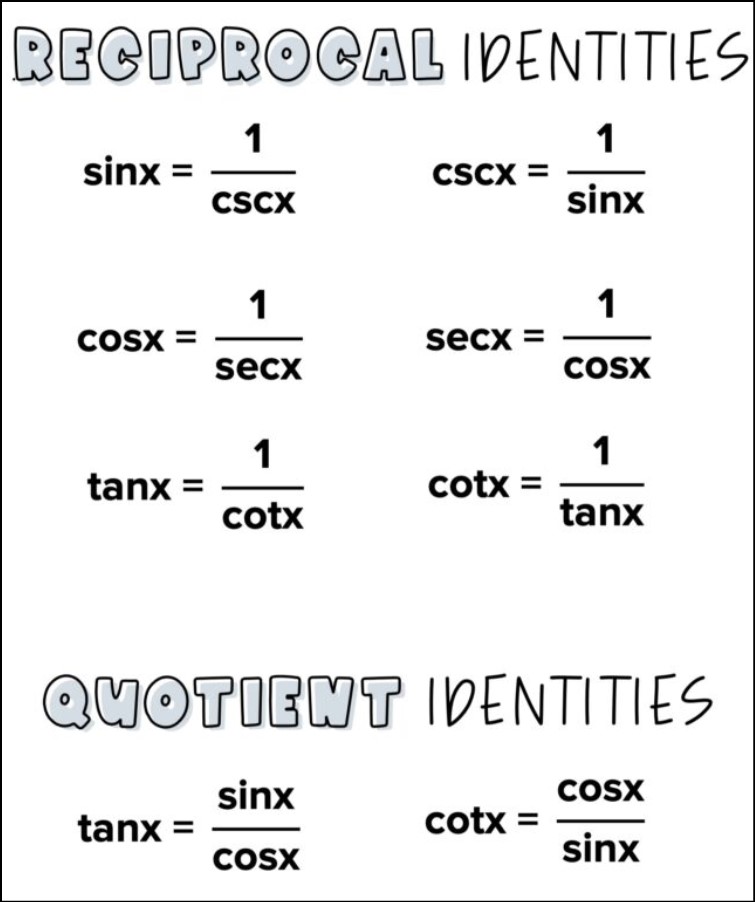
The reciprocal identities derived from the definitions of the six primary trigonometric functions. The sine of an angle in a right triangle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse. Its reciprocal, the cosecant, is the inverse of this ratio. Similarly, the cosine and secant reciprocals of each other, as the tangent and cotangent. These reciprocal relationships can expressed as equations, such as csc(θ) = 1/sin(θ), sec(θ) = 1/cos(θ), and cot(θ) = 1/tan(θ).
Reciprocal identities find extensive applications in solving trigonometric equations, simplifying complex trigonometric expressions, and establishing connections between different trigonometric functions. They particularly useful when working with trigonometric equations involving fractions, as they allow for the transformation of functions into more manageable forms.
Engineers, physicists, and mathematicians often use these identities in fields ranging from physics and engineering to computer graphics and astronomy, where understanding the relationships between trigonometric functions is crucial. Learn How to Find Trigonometric Ratios in Right Triangles
Trigonometry: Reciprocal Identities
Trigonometry, the branch of mathematics concerned with the relationships between the angles and sides of triangles, encompasses a diverse range of identities that interconnect various trigonometric functions. Among these identities, the reciprocal identities hold a special place due to their ability to express one trigonometric function in terms of the reciprocal of another. These identities vital tools for simplifying expressions and solving equations in trigonometry.
Reciprocal identities involve six trigonometric functions: sine (sin), cosine (cos), tangent (tan), cosecant (csc), secant (sec), and cotangent (cot). The reciprocal identities show that the ratio of one function to its reciprocal is always equal to 1. For instance, the sine and cosecant reciprocal identities: sin(θ) = 1/csc(θ) and csc(θ) = 1/sin(θ). Similarly, cos(θ) = 1/sec(θ) and sec(θ) = 1/cos(θ), while tan(θ) = 1/cot(θ) and cot(θ) = 1/tan(θ).
These identities derived from the definitions of trigonometric functions within a right triangle or on the unit circle. They play a fundamental role in simplifying complex trigonometric expressions. By substituting a trigonometric function with its reciprocal identity, mathematicians can transform expressions into more manageable forms. Reciprocal identities also find applications in solving equations, where converting functions to their reciprocal counterparts often leads to solutions.
Reciprocal Identities in Trigonometric Functions
The Reciprocal identities a set of essential relationships that connect various trigonometric functions through their reciprocals. These identities play a pivotal role in trigonometry, enabling mathematicians and scientists to simplify complex expressions, solve equations, and establish connections between different trigonometric functions.
The concept of reciprocal identities arises from the relationships between the sides of a right triangle and the angles within it. For instance, the sine function (sin) is defined as the ratio of the length of the side opposite an angle to the length of the hypotenuse. Its reciprocal, the cosecant function (csc), is the inverse of this ratio. Similar reciprocal relationships exist between cosine and secant, as well as tangent and cotangent.
Reciprocal identities offer a unique way to rewrite trigonometric expressions. By substituting a function with its reciprocal counterpart. Mathematicians can often simplify complex equations, making them easier to manipulate and solve. These identities particularly useful in calculus, where integrals and derivatives involving trigonometric functions can simplified using reciprocal identities.
In real-world applications, reciprocal identities find use in fields like physics, engineering, and architecture. Engineers often employ these identities when dealing with waveforms, oscillations, and rotational motions. In architecture, they can applied to calculate angles and distances, aiding in the design and construction of buildings.