Understanding trigonometric ratios in right triangles is a fundamental concept in mathematics and plays a crucial role in various fields, including engineering, physics, and architecture. Trigonometry involves studying the relationships between the angles and sides of a triangle, especially in right triangles, where one angle measures 90 degrees.
By learning how to find trigonometric ratios in right triangles, you can solve a wide range of real-world problems, from measuring heights and distances to analyzing forces and vectors. In this guide, we will explore the essential trigonometric ratios—sine, cosine, and tangent—and provide step-by-step instructions on how to calculate them in right triangles.
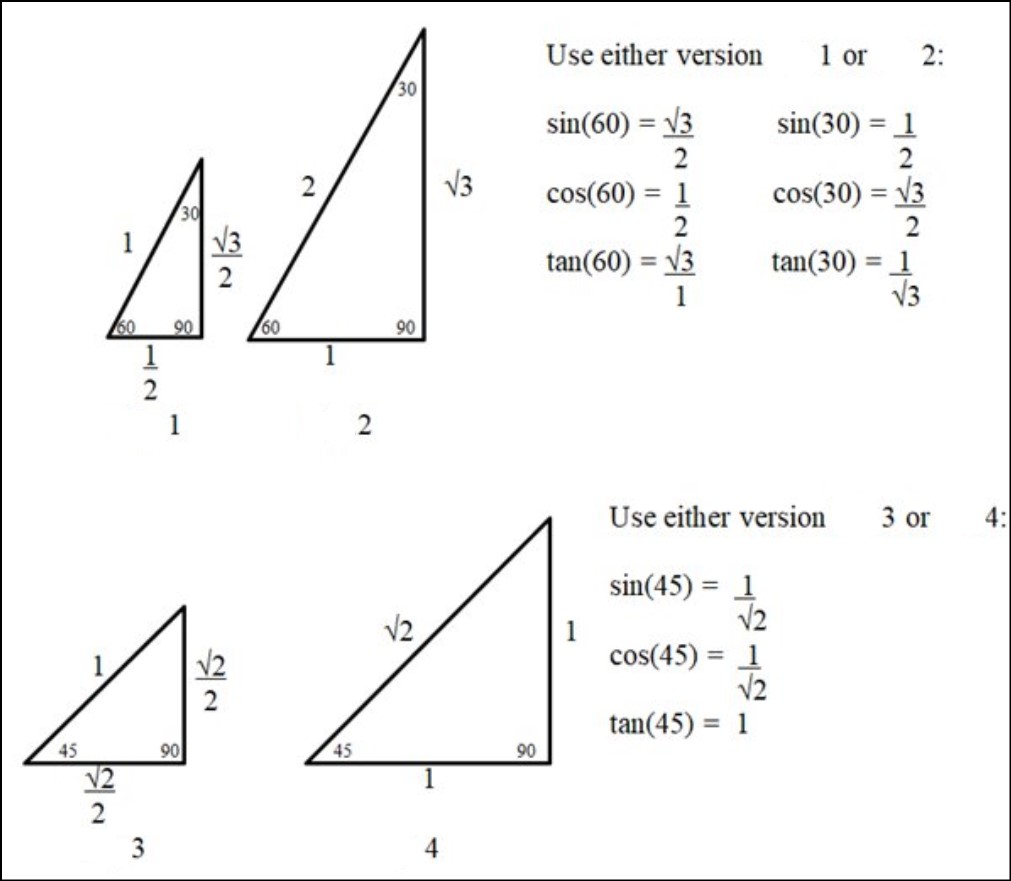
Trigonometric Ratios in Right Triangles
Trigonometric ratios – essential tools in trigonometry that help us understand the relationships between the sides and angles of a right triangle. In a right triangle, which has one angle measuring 90 degrees, there three primary trigonometric ratios: sine (sin), cosine (cos), and tangent (tan). These ratios defined based on the lengths of the sides of the triangle relative to its angles.
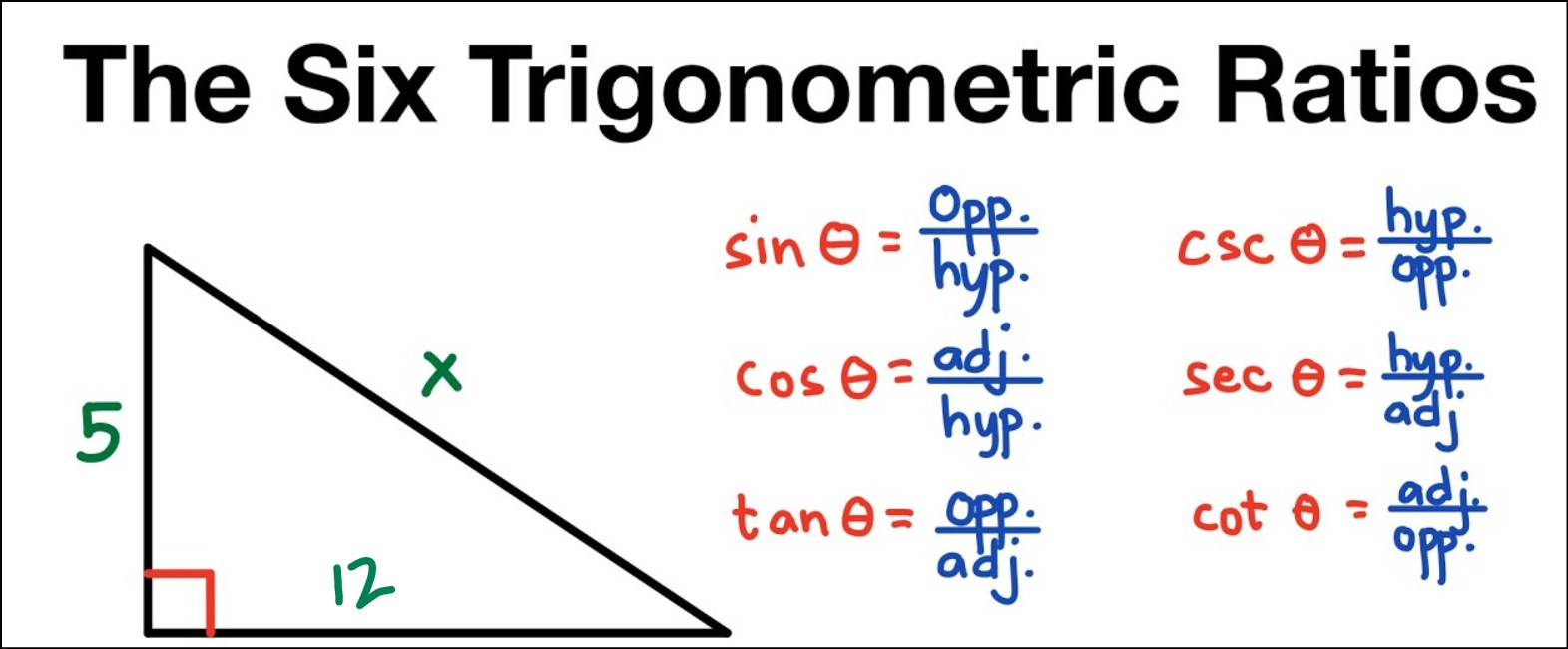
The sine of an angle in a right triangle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse (the side opposite the right angle). The cosine of an angle is the ratio of the length of the adjacent side (the side next to the angle but not the hypotenuse) to the hypotenuse. Lastly, the tangent of an angle is the ratio of the length of the side opposite the angle to the length of the adjacent side.
Trigonometric ratios find applications in various fields, including physics, engineering, architecture, and navigation. By understanding these ratios, we can solve complex problems involving distances, heights, angles, and velocities in right triangles.
How to Find Trigonometric Ratios Given a Right Triangle
To find trigonometric ratios in a right triangle, you need to know the lengths of its sides. Let’s assume we have a right triangle with angles A, B, and C, where C is the right angle. The side opposite angle A is denoted as ‘a,’ the side opposite angle B is denoted as ‘b,’ and the hypotenuse opposite the right angle C is denoted as ‘c.’
To find the sine of angle A, use the formula: sin(A) = a/c. To find the cosine of angle A, use the formula: cos(A) = b/c. And to find the tangent of angle A, use the formula: tan(A) = a/b.
Similarly, for angle B, the formulas would be: sin(B) = b/c, cos(B) = a/c, and tan(B) = b/a.
Remember that these formulas only valid for right triangles. If you have a triangle without a right angle, you’ll need to use different trigonometric concepts.
Trigonometrical Ratios in a Right-Angled Triangle
In a right-angled triangle, the trigonometric ratios play a crucial role in solving various geometric and real-world problems. These ratios, specifically sine, cosine, and tangent, fundamental for trigonometry. In addition to these, other trigonometric ratios like cosecant, secant, and cotangent derived from the primary three.
The sine of an angle in a right triangle is the ratio of the length of the side opposite the angle to the length of the hypotenuse. The cosine of an angle is the ratio of the length of the adjacent side to the hypotenuse. And the tangent of an angle is the ratio of the length of the side opposite the angle to the length of the adjacent side.
Trigonometric ratios used in a wide range of fields, including engineering, physics, astronomy, and even in day-to-day tasks like measuring heights and distances. For example, in surveying, trigonometry helps determine inaccessible distances or heights by measuring angles and applying the appropriate trigonometric ratios.
By understanding these ratios and their applications, mathematicians, scientists, and engineers can solve complex problems related to right-angled triangles and, consequently, various phenomena in the world around us. Trigonometry is a powerful tool that significantly simplifies calculations involving angles and distances in a right triangle context.