The secant function is a fundamental trigonometric function that holds various identities essential in trigonometry. Among these identities, the “Sec Trig Identity” specifically deals with the square of the secant function. Understanding this identity crucial for solving complex trigonometric equations and mathematical problems involving secant functions.
Sec Trig Identity
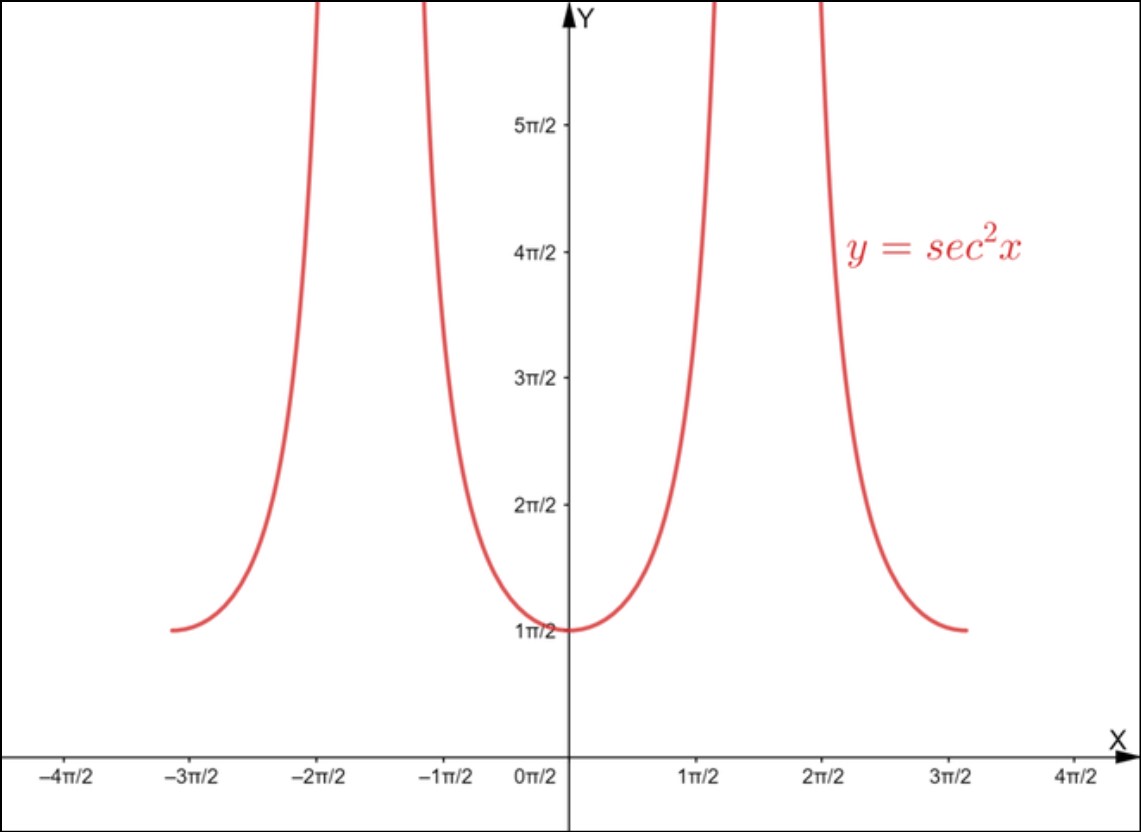
The secant trigonometric identity is a fundamental relationship in trigonometry that involves the secant function, denoted as sec(x). The secant function is the reciprocal of the cosine function, which means sec(x) = 1/cos(x). This identity is derived from the Pythagorean trigonometric identity, which states that sin^2(x) + cos^2(x) = 1. By dividing both sides of this equation by cos^2(x), we get sec^2(x) – 1 = tan^2(x). Another way to represent this identity is sec^2(x) = 1 + tan^2(x).
The secant trig identity has various applications in mathematics, physics, and engineering. It often used to simplify complex trigonometric expressions and solve trigonometric equations. Additionally, the secant function plays a crucial role in the study of periodic phenomena, such as the oscillations of a pendulum or the behavior of alternating currents in electrical circuits. In calculus, this identity employed to evaluate integrals involving the secant function, especially in trigonometric substitutions.
Furthermore, the secant trig identity indispensable in solving right-angled triangles. And determining the lengths of sides or measures of angles. It an essential tool in trigonometry, as it allows for seamless conversions. Between trigonometric functions and simplifies their manipulation in various mathematical contexts. Understanding and applying the secant trig identity crucial for students and professionals. In fields like engineering, physics, surveying, and astronomy, where trigonometry extensively utilized.
In summary, the secant trig identity, derived from the Pythagorean identity, establishes a vital connection between the secant function and the tangent function. It finds widespread application in mathematics and various scientific disciplines. providing a powerful tool to solve trigonometric problems, simplify expressions, and analyze periodic phenomena. Learn More Trigonometry:- Sum and Difference Trig Identities
Sec Squared Formula
The sec squared formula a trigonometric identity that expresses sec^2(x). The square of the secant function, in terms of the other two primary trigonometric functions, sine and cosine. The secant squared formula derived from the definition of the secant function as sec(x) = 1/cos(x). But by squaring both sides of this equation, we obtain sec^2(x) = 1/cos^2(x). Using the Pythagorean trigonometric identity, sin^2(x) + cos^2(x) = 1, we can rewrite the equation as sec^2(x) = 1 + tan^2(x).
The sec squared formula has numerous applications in calculus, engineering, physics, and other fields involving trigonometry. It frequently used to simplify expressions containing secant functions or to transform trigonometric equations into more manageable forms. In calculus, the sec squared formula plays a significant role in integration problems, especially when dealing with integrals that involve secant functions. Trigonometric substitutions using this identity often lead to elegant solutions for complex integrals.
Moreover, the sec squared formula essential in understanding the behavior of periodic functions and oscillatory phenomena. It helps in analyzing the amplitudes and frequencies of waves, such as sound waves, electromagnetic waves, and mechanical vibrations. In engineering and physics, this identity applied in fields like signal processing, communications, and structural dynamics.
In conclusion, the sec squared formula a powerful trigonometric identity that simplifies expressions involving the secant function. Its applications extend across various mathematical and scientific disciplines, making it a valuable tool for solving problems, analyzing periodic behavior, and evaluating integrals.
Square of Secant Function Identity
The square of the secant function identity is a trigonometric relationship that concerns the square of the secant function, denoted as sec^2(x). It is derived from the Pythagorean trigonometric identity, which states that sin^2(x) + cos^2(x) = 1. But by dividing both sides of the Pythagorean identity by cos^2(x), we get sec^2(x) – 1 = tan^2(x). This equation can rearranged to give the square of the secant function identity as sec^2(x) = 1 + tan^2(x).
The square of the secant function identity has numerous applications in trigonometry, calculus, and physics. It is commonly used to simplify expressions containing secant functions and to manipulate trigonometric equations. In calculus, this identity often arises when dealing with integrals that involve secant functions. Trigonometric substitutions using the square of the secant function identity can help to solve complex integrals, especially those with radical terms.
Additionally, the square of the secant function identity is crucial in understanding the properties of periodic functions and wave phenomena. It is extensively applied in physics, engineering, and signal processing to analyze the behavior of waves, such as electromagnetic waves, sound waves, and seismic waves.
Moreover, the square of the secant function identity plays a significant role in solving problems. Involving right-angled triangles and trigonometric ratios. It is an essential tool in trigonometry and finds application in fields like astronomy, navigation, and architecture. Where accurate measurements and calculations of angles and distances necessary.
To sum up, the square of the secant function identity is a fundamental trigonometric relationship that allows for simplification of expressions and the solution of various trigonometric problems. Its applications span across mathematics, physics, engineering, and other scientific disciplines, making it an invaluable tool for researchers, students, and professionals alike.