Trig Identities Sin Cos: Trigonometric identities involving sine and cosine play a fundamental role in mathematics, especially in calculus and physics. These identities, such as the Pythagorean Identity and the double-angle identity, allow us to simplify complex trigonometric expressions and solve a variety of mathematical problems. Additionally, integration using trigonometric identities or trig substitution is a powerful technique that aids in finding solutions to challenging integrals involving trigonometric functions. In this article, we will explore the significance of trig identities involving sin and cos and delve into the application of trigonometric substitution in integration.
Trig Identities Sin Cos
Trigonometric identities fundamental equations that relate different trigonometric functions. Two of the most commonly used trig identities involve sine (sin) and cosine (cos). These identities essential in various branches of mathematics, especially in calculus and physics. The first identity is the Pythagorean Identity, which states that for any angle ‘θ’ in a right triangle, the sum of the squares of sine and cosine is always equal to one. Mathematically, it is expressed as sin^2(θ) + cos^2(θ) = 1.
Another crucial trig identity involving sine and cosine is the double-angle identity. This identi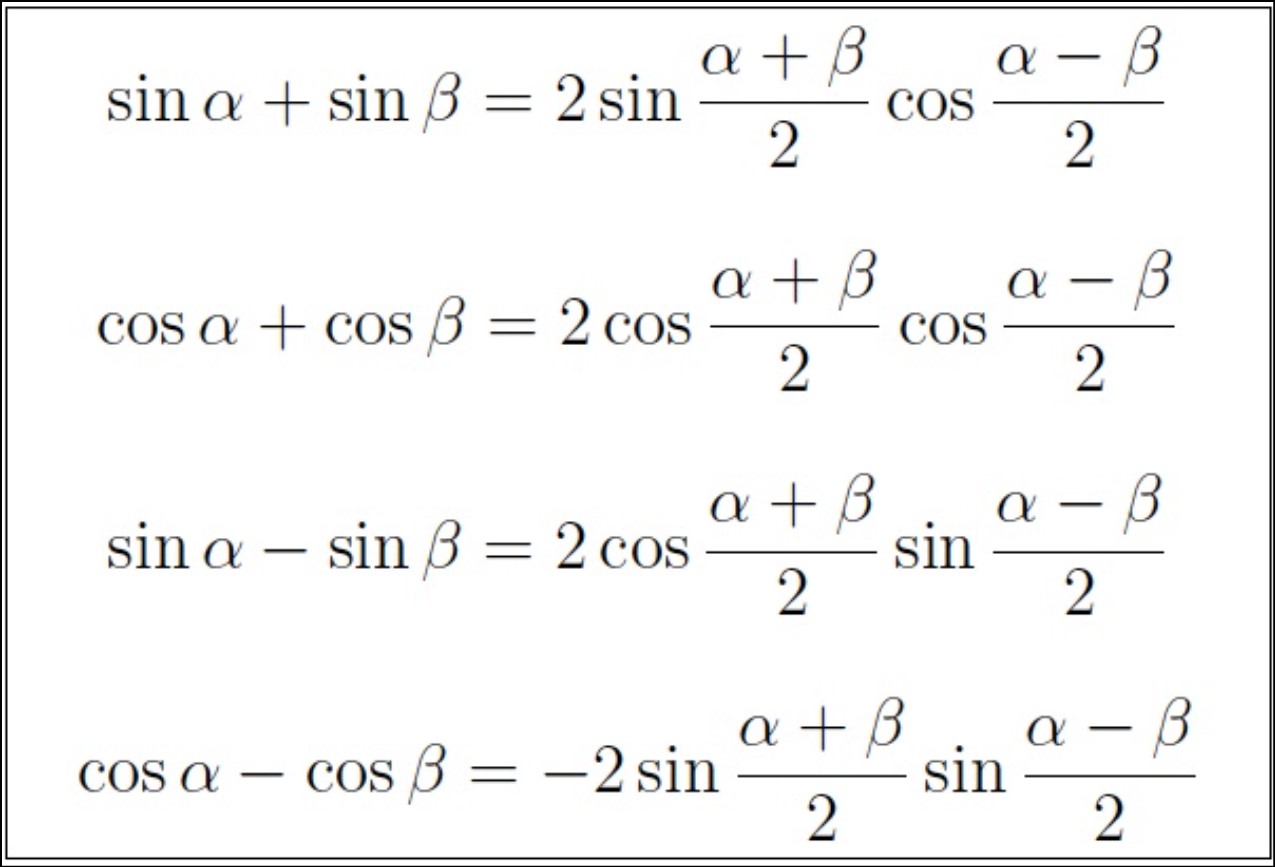
ty allows us to express trigonometric functions of double angles in terms of the original angle. For example, the double-angle identity for sine is sin(2θ) = 2sin(θ)cos(θ), and for cosine, it is cos(2θ) = cos^2(θ) – sin^2(θ).
In calculus, these trig identities play a vital role in simplifying complex expressions, solving trigonometric equations, and evaluating limits. They also extensively used in trigonometric substitution, which helps in solving integrals involving radical functions. Understanding and mastering trig identities involving sine and cosine crucial for success in higher mathematics and various STEM fields. Learn How to Verify Trig Identities
Trig Identity for cos(t) + sin(t)
One of the most frequently used trigonometric identities involves the sum of cosine and sine of the same angle ‘t.’ The identity is as follows: cos(t) + sin(t) = √2 * sin(t + π/4).
This identity is derived by using the concept of rotational angles and the Pythagorean Identity. When we add cos(t) and sin(t), we can interpret it as the coordinates (x, y) of a point on the unit circle corresponding to an angle ‘t.’ Using the Pythagorean Identity (sin^2(t) + cos^2(t) = 1), we can find the magnitude of the resulting vector. Then, by considering the angle formed between the positive x-axis and the resultant vector (t + π/4), we get the simplified form √2 * sin(t + π/4).
This trigonometric identity finds applications in various mathematical problems, such as solving differential equations, evaluating certain integrals, and analyzing periodic functions. It also plays a significant role in physics, engineering, and signal processing, where harmonic functions common.
Integration Using Trig Identities or a Trig Substitution
Integration is a fundamental concept in calculus, allowing us to find the area under curves and solve various real-world problems. Trigonometric identities and trigonometric substitution powerful techniques that aid in solving challenging integrals involving trigonometric functions.
Trigonometric identities, such as the Pythagorean Identity (sin^2(θ) + cos^2(θ) = 1) and the double-angle identities, can used to simplify complex integrals. By using these identities, we can convert trigonometric expressions into simpler forms that easier to integrate. This technique is particularly useful when dealing with integrals containing expressions like sin^2(x) or cos^2(x).
Trigonometric substitution, on the other hand, is a method that involves replacing a variable in an integral with a trigonometric expression. This technique is especially valuable when dealing with integrals that contain square roots of quadratic expressions or the sum/difference of squares. By making a suitable trigonometric substitution, the integral can transformed into a more manageable form, often leading to straightforward solutions.
Both trigonometric identities and trigonometric substitution crucial tools in solving a wide range of integrals. Students and professionals in mathematics, physics, and engineering frequently encounter these methods when working with complex mathematical models and real-world applications. Mastery of these techniques is essential for tackling advanced problems in calculus and related fields.