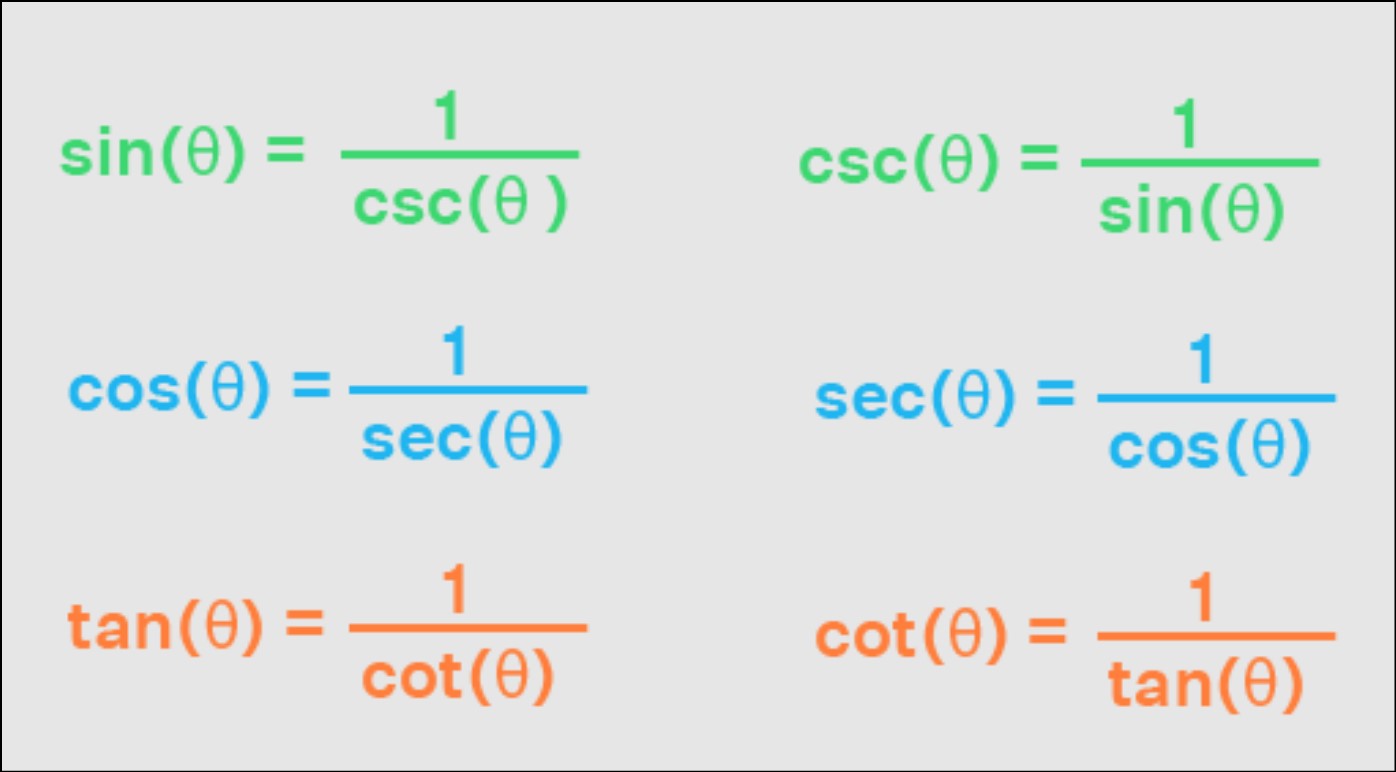Squared Trig Identities, also known as Squared Trigonometric Functions, are fundamental mathematical relationships that involve squaring trigonometric functions or expressing them in terms of other trigonometric functions. These identities play a pivotal role in trigonometry, providing valuable tools for simplifying complex expressions, solving trigonometric equations, and gaining deeper insights into the behavior of trigonometric functions.
Squared Trig Identities
Squared trigonometric identities involve squaring trigonometric functions or expressing squared trigonometric functions in terms of other trigonometric functions. These identities are useful in simplifying complex expressions and solving trigonometric equations.
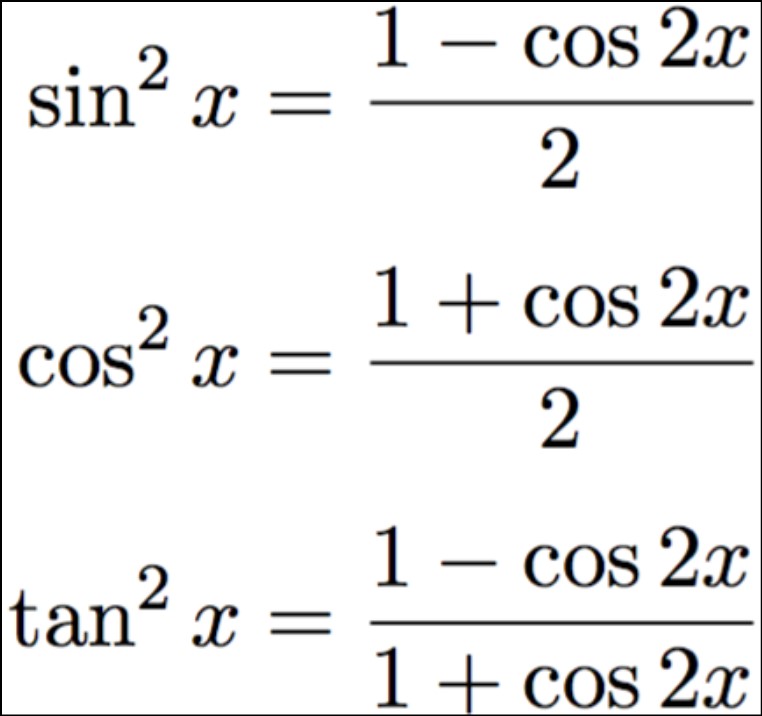
Here are some fundamental squared trigonometric identities:
1.1. Pythagorean Identity: One of the most well-known squared trigonometric identities is the Pythagorean identity, which relates the squares of the sine and cosine functions. It states that for any angle θ:
sin²θ + cos²θ = 1
1.2. Double Angle Formulas: The double angle formulas involve the squared trigonometric functions of angles that are double the given angle. For example:
sin(2θ) = 2sinθcosθ
cos(2θ) = cos²θ – sin²θ
1.3. Half Angle Formulas: The half angle formulas express the squared trigonometric functions of angles that are half the given angle. These formulas are useful in integration and solving trigonometric equations. For example:
sin²(θ/2) = (1 – cosθ) / 2
cos²(θ/2) = (1 + cosθ) / 2
1.4. Sum and Difference Formulas: The sum and difference formulas for squared trigonometric functions express the square of the sum or difference of two angles in terms of the squares of the individual angles. For example:
sin(α + β)² = sin²α + 2sinαsinβ + sin²β
cos(α – β)² = cos²α + 2cosαcosβ + cos²β
These squared trigonometric identities form the foundation for more complex trigonometric manipulations and are essential in many mathematical applications. Learn More Trigonometry:- Trigonometry Quadrant with Formulas
Identities of Squared Trigonometric Functions
Squared trigonometric functions are expressions where a trigonometric function is squared, such as sin²θ, cos²θ, tan²θ, etc. These identities are crucial in various fields, including physics, engineering, and calculus. Understanding these identities allows us to simplify trigonometric expressions, solve equations more efficiently, and gain insights into the behavior of trigonometric functions.
Here are some notable identities of squared trigonometric functions:
2.1. Reciprocal Identities: The reciprocal identities involve the squared trigonometric functions in the denominator. For example:
csc²θ = 1/sin²θ
sec²θ = 1/cos²θ
cot²θ = 1/tan²θ
2.2. Sum and Difference Identities: Similar to squared trigonometric identities, sum and difference identities also exist for squared trigonometric functions. For example:
sin²(α + β) = sin²α + 2sinαsinβ + sin²β
cos²(α – β) = cos²α + 2cosαcosβ + cos²β
2.3. Double Angle Identities: Double angle identities for squared trigonometric functions help express the squares of double angles in terms of the original angle. For example:
sin²(2θ) = 4sin²θcos²θ
cos²(2θ) = 2cos²θ – 1
2.4. Half Angle Identities: The half-angle identities for squared trigonometric functions allow us to express the squares of half angles in terms of the original angle. For example:
sin²(θ/2) = (1 – cosθ) / 2
cos²(θ/2) = (1 + cosθ) / 2
By mastering these identities, mathematicians, scientists, and engineers can manipulate trigonometric expressions with confidence and apply them to various problem-solving scenarios.
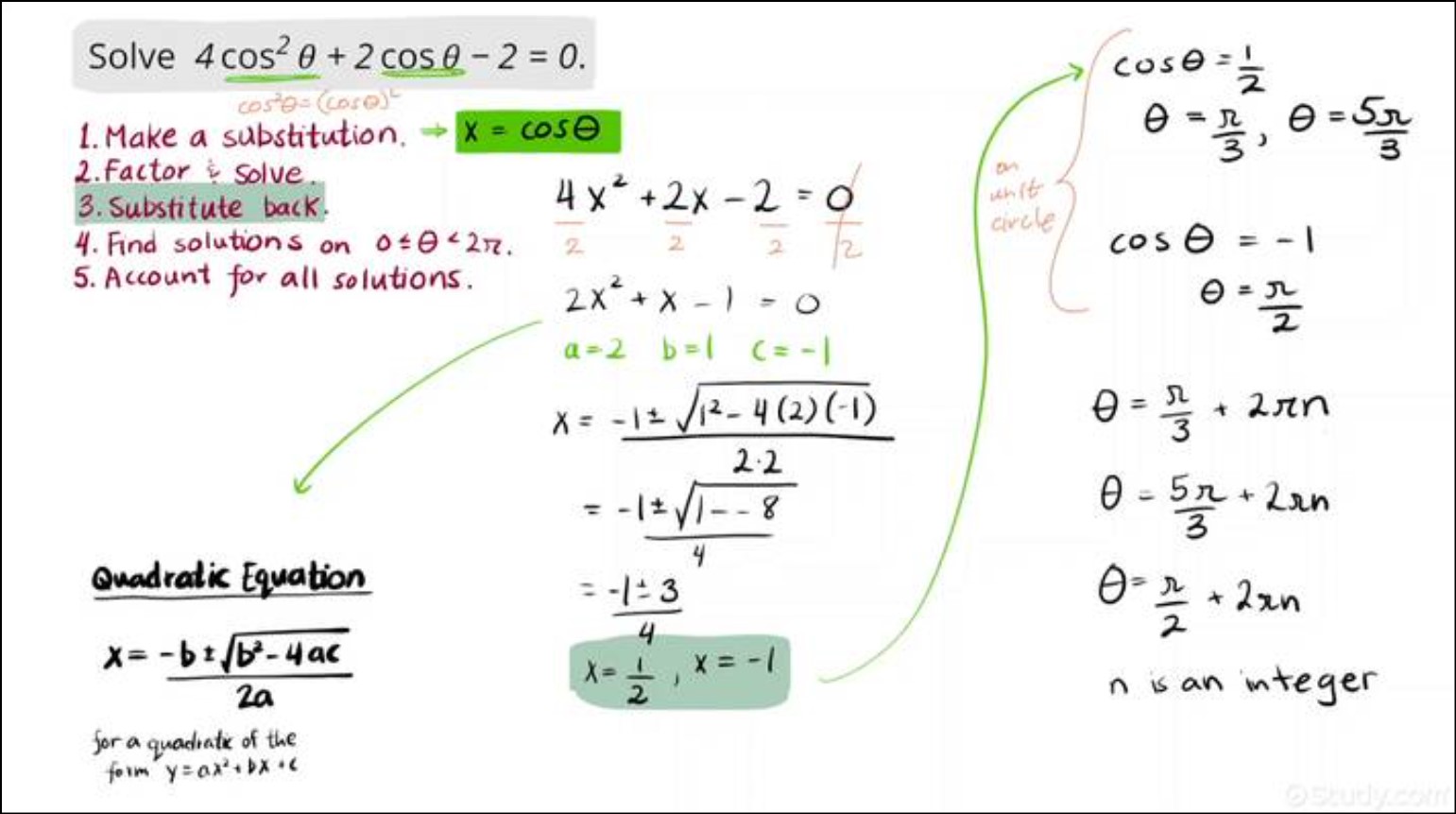
How to Solve Trigonometric Equations with a Squared Function with the Square Root Property
Solving trigonometric equations involving squared functions is a common task in mathematics and physics. One effective method to solve such equations is by using the square root property. The square root property states that if x² = a, then x = ±√a, where ‘a’ is a constant.
Here’s a step-by-step guide on how to use the square root property to solve trigonometric equations with a squared function:
3.1. Isolate the squared function: Rewrite the given trigonometric equation in a way that you have a squared function on one side of the equation. For example, consider the equation sin²θ = 1/4.
3.2. Apply the square root property: Take the square root of both sides of the equation. Don’t forget to consider both the positive and negative square roots. Using the example from step 1:
sinθ = ±√(1/4)
sinθ = ±1/2
3.3. Find all solutions: Trigonometric functions have periodicity, meaning they repeat after certain intervals (e.g., 360 degrees or 2π radians). To find all solutions, consider the general solutions for the trigonometric function involved. In our example, the solutions are:
θ = 30° + 360°n
θ = 150° + 360°n
θ = 210° + 360°n
θ = 330° + 360°n
Where ‘n’ is an integer.
3.4. Check for extraneous solutions: After obtaining the solutions, check if they satisfy the original equation. In some cases, the solutions obtained may not be valid due to the domain restrictions of the squared trigonometric functions. Eliminate any solutions that do not satisfy the original equation.
By following these steps and practicing with various examples, you can confidently solve trigonometric equations involving squared functions using the square root property.
Reciprocal, Quotient and Square Relations
Trigonometric functions have various interrelated properties that form the basis for solving complex trigonometric problems. Among these, reciprocal, quotient, and square relations are particularly important. Understanding these relations allows us to simplify trigonometric expressions, manipulate equations, and find connections between different trigonometric functions.
4.1. Reciprocal Relations: The reciprocal relations involve the reciprocal trigonometric functions, such as secant (sec), cosecant (csc), and cotangent (cot). These are defined as the reciprocals of cosine, sine, and tangent, respectively. The reciprocal relations are as follows:
sec(θ) = 1 / cos(θ)
csc(θ) = 1 / sin(θ)
cot(θ) = 1 / tan(θ)
4.2. Quotient Relations: The quotient relations involve the tangent (tan) function and its reciprocal, cotangent (cot). The quotient relations are as follows:
tan(θ) = sin(θ) / cos(θ)
cot(θ) = cos(θ) / sin(θ)
4.3. Square Relations: Square relations involve squaring trigonometric functions or expressing squared trigonometric functions in terms of other trigonometric functions. For example, the Pythagorean identity is a square relation that relates the squares of sine and cosine:
sin²(θ) + cos²(θ) = 1
4.4. Connection between Reciprocal and Quotient Relations: Reciprocal relations are related to quotient relations through the reciprocal identity. For example:
csc(θ) = 1 / sin(θ)
csc(θ) = 1 / (1 / cot(θ))
csc(θ) = cot(θ)
Understanding these reciprocal, quotient, and square relations is essential in simplifying complex trigonometric expressions and solving trigonometric equations. These relationships form the building blocks for more advanced trigonometric concepts and play a crucial role in various scientific and engineering applications.