Calculus Trig Identities: Calculus, a fundamental branch of mathematics, delves into the study of change and motion. In the realm of calculus, trigonometric identities play a crucial role in simplifying complex functions involving trigonometric expressions. By understanding how to manipulate these identities, one gains valuable tools for solving derivatives and integrals involving trigonometric functions. This article explores the world of Calculus Trig Identities, shedding light on their significance in both derivatives and integrals.
Calculus Trig Identities
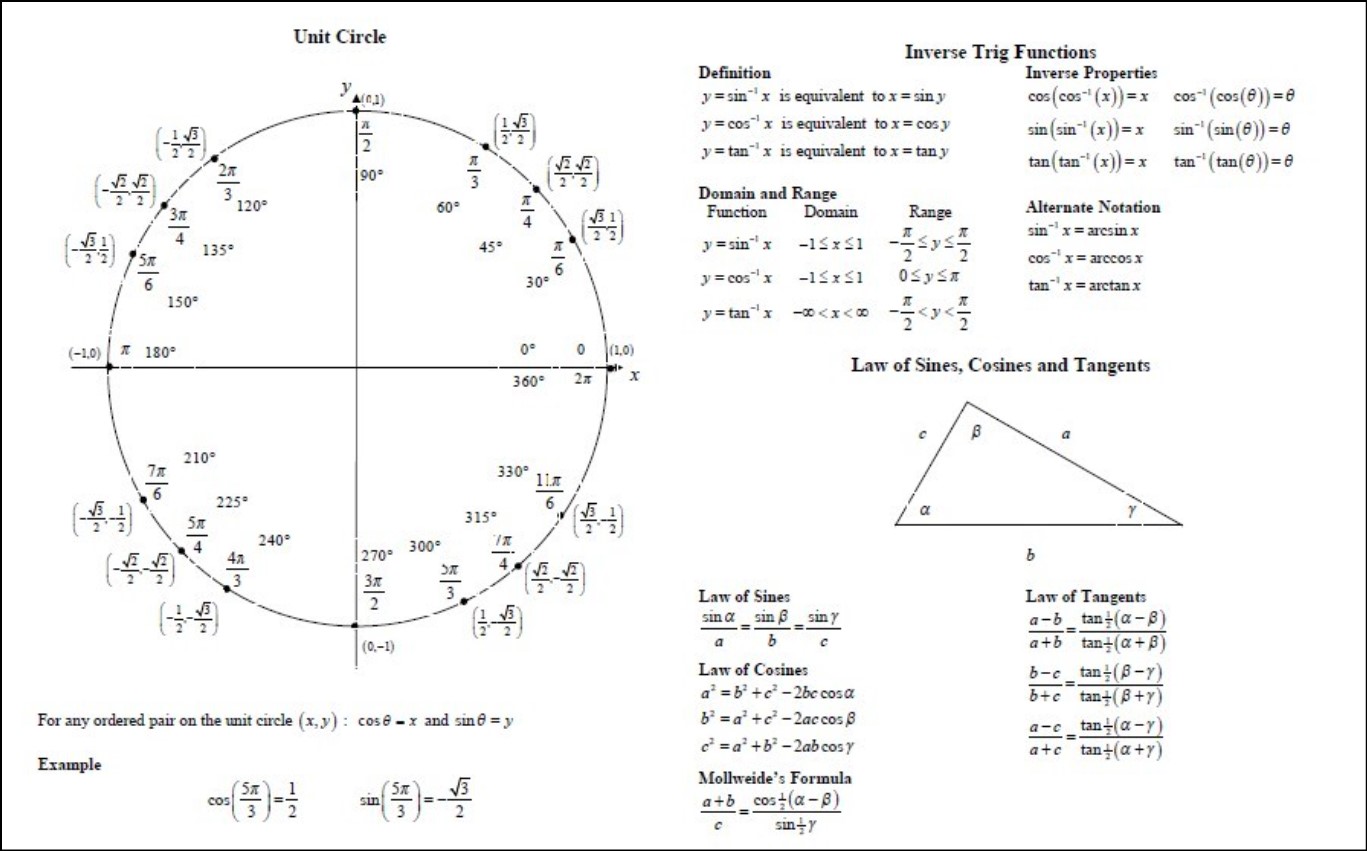
Calculus involves the study of change and motion, and trigonometric identities play a crucial role in simplifying complex trigonometric expressions that frequently appear in calculus problems. Trigonometric identities are fundamental equations that establish relationships between trigonometric functions. These identities are vital tools for solving integrals, derivatives, and other calculus problems involving trigonometric functions.
One of the most fundamental trigonometric identities is the Pythagorean identity: sin²θ + cos²θ = 1. This identity relates the sine and cosine functions and is derived from the Pythagorean theorem. It forms the basis for many other trigonometric identities. Another crucial identity is the sum and difference identity for sine and cosine functions, which helps in breaking down complex trigonometric expressions into simpler ones.
In calculus, trigonometric identities are used to evaluate limits, solve differential equations involving trigonometric functions, and simplify integrals. They also aid in expressing trigonometric functions in terms of one another, leading to more manageable forms for calculations. Additionally, trigonometric identities are essential in the study of power series expansions and Fourier series, which are extensively used in advanced calculus and mathematical physics.
It is crucial for students of calculus to master these trigonometric identities, as they form the foundation for solving more complex problems. By understanding these identities, students can tackle a wide range of calculus problems more effectively and gain a deeper insight into the intricate relationships between trigonometric functions. Learn More Trigonometry:- Even Odd Trig Identities with Examples & Explanation
Trig Identities for Pre-Calculus
Before diving into calculus, students are typically introduced to trigonometry concepts in pre-calculus courses. Trigonometric identities play a significant role in pre-calculus, providing students with the tools to simplify expressions and solve equations involving trigonometric functions.
In pre-calculus, students learn about basic trigonometric identities, such as the reciprocal identities, quotient identities, and Pythagorean identities. Reciprocal identities, such as csc(θ) = 1/sin(θ) and sec(θ) = 1/cos(θ), express trigonometric functions in terms of their reciprocals. Quotient identities, like tan(θ) = sin(θ)/cos(θ), relate the tangent function to sine and cosine. These identities are crucial for simplifying trigonometric expressions and solving trigonometric equations.
Pre-calculus students also encounter sum and difference identities, double-angle identities, and half-angle identities. These identities allow them to manipulate trigonometric functions in various ways, making it easier to evaluate trigonometric expressions and equations. Understanding these identities enables students to solve problems involving angles and trigonometric functions in real-world applications, such as physics, engineering, and architecture.
Moreover, pre-calculus lays the groundwork for more advanced calculus topics, where trigonometric functions are heavily utilized. By mastering trigonometric identities at this stage, students build a solid foundation. For tackling more complex calculus concepts involving trigonometric functions in the future.
Calculus Trigonometric Derivatives and Integrals
In calculus, the study of trigonometric derivatives and integrals is essential for understanding the behavior of trigonometric functions and their applications. Derivatives of trigonometric functions help determine rates of change, slopes, and concavity, while trigonometric integrals are vital for finding areas under curves and evaluating accumulated quantities.
The derivatives of basic trigonometric functions follow specific patterns. For instance, the derivative of sin(θ) is cos(θ), and the derivative of cos(θ) is -sin(θ). The derivatives of tangent, cotangent, secant, and cosecant functions can be obtained using quotient rule and chain rule techniques. These derivatives are crucial in physics, engineering. And other fields where rates of change and dynamic behavior are of interest.
Integrating trigonometric functions involves finding antiderivatives and computing definite integrals. Techniques like substitution and integration by parts are commonly used to solve trigonometric integrals. These integrals arise in various physics problems, such as calculating work done by a force. Or finding the center of mass of an object with non-uniform density.
Trigonometric derivatives and integrals are interconnected through fundamental theorems of calculus, such as the Fundamental Theorem of Calculus and the chain rule for integration. These theorems establish the relationship between derivatives and integrals, enabling the evaluation of integrals using antiderivatives.
In summary, understanding trigonometric derivatives and integrals is essential for students of calculus. Proficiency in these topics allows students to solve a wide range of problems in calculus, physics, engineering, and many other fields where trigonometric functions and their properties are prevalent.