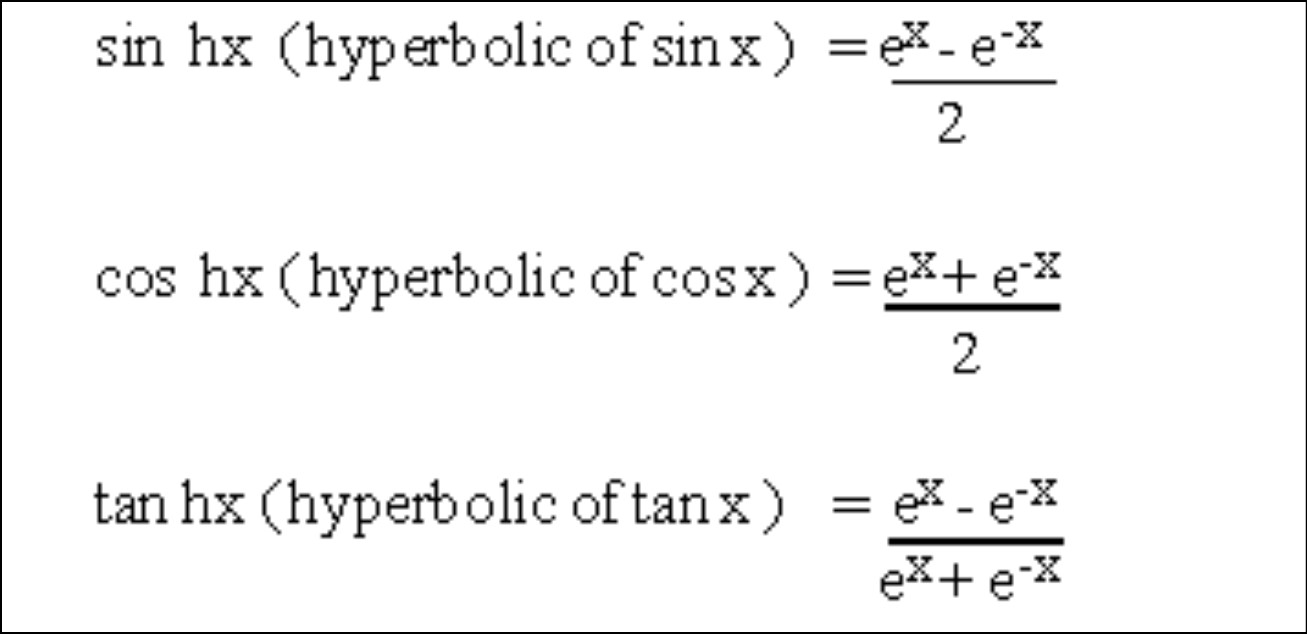Hyperbolic Trig Identities, formulas, and functions essential mathematical tools used in various fields, including calculus, physics, engineering, and more. These identities the hyperbolic counterparts of the standard trigonometric identities, involving hyperbolic sine, hyperbolic cosine, hyperbolic tangent, and other hyperbolic functions.
Understanding these identities enables us to solve complex problems involving hyperbolic functions and facilitates the simplification of expressions in hyperbolic trigonometry. In this article, we will explore the key hyperbolic trigonometric identities, formulas, and functions, along with their applications in real-world scenarios.
Hyperbolic Trig Identities
Hyperbolic trigonometry deals with the hyperbolic functions, which analogs of the circular trigonometric functions. These functions arise in various mathematical and scientific applications, especially in areas such as physics, engineering, and calculus. Hyperbolic trig identities essential tools that help simplify and manipulate hyperbolic expressions. They analogous to the familiar trigonometric identities but involve the hyperbolic sine (sinh), hyperbolic cosine (cosh), hyperbolic tangent (tanh), hyperbolic cotangent (coth), hyperbolic secant (sech), and hyperbolic cosecant (csch).
One of the fundamental hyperbolic trig identities is the hyperbolic Pythagorean identity: cosh^2(x) - sinh^2(x) = 1. This identity bears resemblance to the Pythagorean identity in circular trigonometry, but here we deal with hyperbolic functions. Another useful identity is the hyperbolic addition formula for the hyperbolic tangent: tanh(x + y) = (tanh(x) + tanh(y)) / (1 + tanh(x)*tanh(y)). This formula allows us to express the tangent of the sum of two angles in terms of their individual tangents.
Furthermore, we have the hyperbolic double-angle formulas, such as cosh(2x) = cosh^2(x) + sinh^2(x) and sinh(2x) = 2 * sinh(x) * cosh(x), which bear similarity to the circular trigonometric double-angle identities. Additionally, there hyperbolic half-angle formulas, inverse hyperbolic trig identities, and many more that aid in solving complex problems involving hyperbolic functions.
In summary, hyperbolic trig identities powerful tools in hyperbolic trigonometry, allowing mathematicians and scientists to simplify expressions, derive new formulas, and solve a wide range of problems across various fields of study. Learn How to Verify Trig Identities
List of Hyperbolic Trigonometry Functions
Hyperbolic trigonometry involves a set of six primary hyperbolic functions, each of which has analogs in circular trigonometry.
These functions essential for understanding and solving problems related to hyperbolic geometry and various applications in science and mathematics.
- Hyperbolic Sine (sinh). Defined as
sinh(x) = (e^x - e^(-x)) / 2, the hyperbolic sine is an odd function that represents the relationship between the sides of a hyperbolic right triangle. - Hyperbolic Cosine (cosh). Given by
cosh(x) = (e^x + e^(-x)) / 2, the hyperbolic cosine is an even function and plays a vital role in hyperbolic geometry. - Hyperbolic Tangent (tanh). The hyperbolic tangent is defined as
tanh(x) = sinh(x) / cosh(x). It is one of the most frequently used hyperbolic functions, appearing in many scientific applications. - Hyperbolic Cotangent (coth). Coth(x) is the reciprocal of tanh(x), i.e.,
coth(x) = 1 / tanh(x). It finds applications in various engineering and physics problems. - Hyperbolic Secant (sech). The hyperbolic secant is given by
sech(x) = 1 / cosh(x), and it is used in fields like signal processing and quantum mechanics. - Hyperbolic Cosecant (csch). The hyperbolic cosecant function is defined as
csch(x) = 1 / sinh(x), playing a significant role in hyperbolic function identities and calculations.
These six functions form the foundation of hyperbolic trigonometry, and by combining them with hyperbolic identities and formulas, mathematicians and scientists can analyze complex systems and phenomena more effectively.
Hyperbolic Function Identities
Hyperbolic function identities essential mathematical relationships that involve hyperbolic trigonometry functions. These identities used to simplify expressions, solve equations, and manipulate hyperbolic functions in various mathematical and scientific contexts.
Some of the key hyperbolic function identities include:
- Hyperbolic Pythagorean Identity.
cosh^2(x) - sinh^2(x) = 1. This identity is analogous to the Pythagorean identity in circular trigonometry and plays a fundamental role in hyperbolic geometry. - Hyperbolic Addition and Subtraction Formulas. Similar to circular trigonometry, hyperbolic functions have addition and subtraction formulas. For instance,
cosh(x + y) = cosh(x) * cosh(y) + sinh(x) * sinh(y)andsinh(x + y) = sinh(x) * cosh(y) + cosh(x) * sinh(y). - Hyperbolic Double-Angle Formulas. These formulas express hyperbolic functions of double angles in terms of the hyperbolic functions of the original angle. For example,
cosh(2x) = cosh^2(x) + sinh^2(x)andsinh(2x) = 2 * sinh(x) * cosh(x). - Inverse Hyperbolic Function Identities. Inverse hyperbolic functions allow us to find the angle corresponding to a given hyperbolic function value. For instance,
arcsinh(x) = ln(x + sqrt(x^2 + 1))andarccosh(x) = ln(x + sqrt(x^2 - 1)). - Hyperbolic Half-Angle Formulas. These identities express hyperbolic functions of half angles in terms of the hyperbolic functions of the original angle. For example,
sinh(x/2) = sqrt((cosh(x) - 1) / 2).
These identities, along with the basic properties of hyperbolic functions, form the backbone of hyperbolic trigonometry, aiding in solving complex problems in various fields.
Hyperbolic Functions Formula
Hyperbolic functions defined using exponential functions, making them closely related to exponential growth and decay. The primary hyperbolic functions the hyperbolic sine (sinh) and hyperbolic cosine (cosh), which derived from the exponential function e^x.
The formulas for these functions as follows:
- Hyperbolic Sine (sinh).
sinh(x) = (e^x - e^(-x)) / 2. The hyperbolic sine represents the relationship between the sides of a hyperbolic right triangle and exhibits exponential growth as x increases. - Hyperbolic Cosine (cosh).
cosh(x) = (e^x + e^(-x)) / 2. The hyperbolic cosine is an even function and also demonstrates exponential growth as x increases.
The other hyperbolic functions can derived from these two primary functions. For example, the hyperbolic tangent (tanh) is defined as the ratio of the hyperbolic sine to the hyperbolic cosine: tanh(x) = sinh(x) / cosh(x). Similarly, the hyperbolic cotangent (coth) is the reciprocal of the hyperbolic tangent: coth(x) = 1 / tanh(x). The hyperbolic secant (sech) is the reciprocal of the hyperbolic cosine: sech(x) = 1 / cosh(x), and the hyperbolic cosecant (csch) is the reciprocal of the hyperbolic sine: csch(x) = 1 / sinh(x).
These formulas not only define the hyperbolic functions but also illustrate their close connection to exponential functions. The exponential growth and decay nature of hyperbolic functions often makes them applicable in a wide range of real-world scenarios. For example, when modeling the spread of infectious diseases or describing population growth, hyperbolic functions can accurately represent such processes.