Even Odd Trig Identities: The concept of even odd trig identities is an essential aspect of trigonometry, enabling the simplification and manipulation of trigonometric expressions. These identities categorize trigonometric functions as either even or odd based on their unique symmetry properties.
In this discussion, examples and explanations of even odd trig identities will be presented, shedding light on the properties of popular trigonometric functions like cosine, sine, tangent, secant, cosecant, and cotangent. By delving into these examples, readers will gain a deeper understanding of how even odd trig identities can be applied to streamline mathematical calculations and problem-solving in the realm of trigonometry.
Even Odd Trig Identities
Trigonometric identities play a crucial role in simplifying and solving trigonometric equations. Among these identities, the even-odd trigonometric identities are particularly useful and have unique properties. An even function is one that satisfies the property f(-x) = f(x), while an odd function satisfies f(-x) = -f(x). Let’s explore some common even odd trig identities.
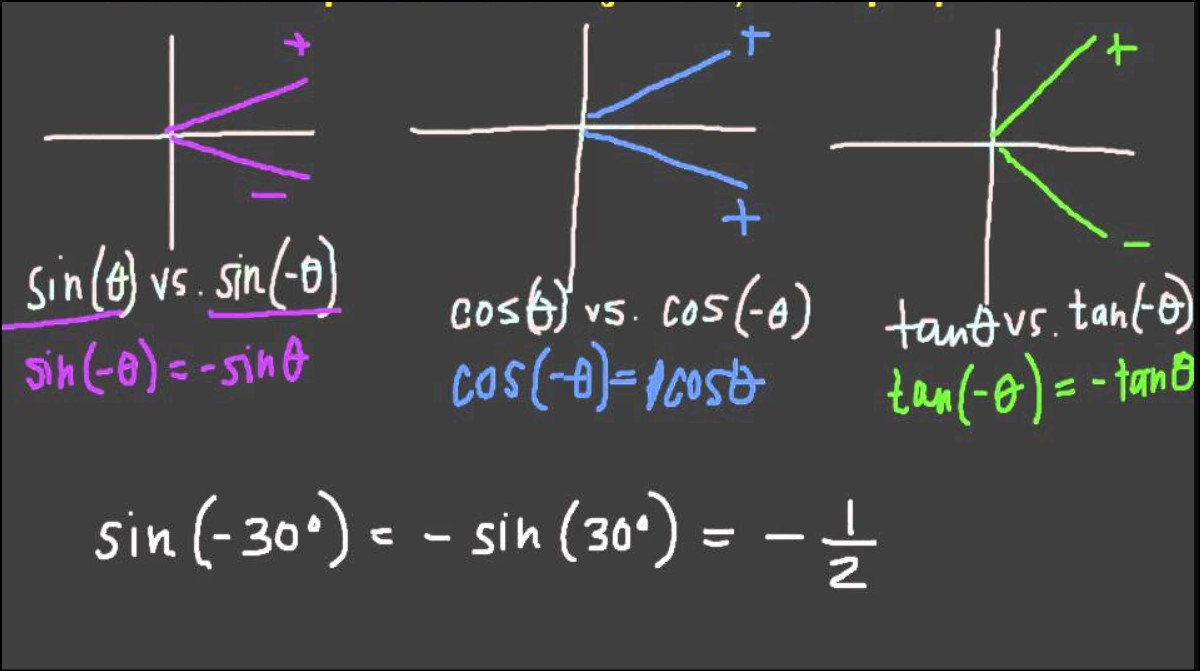
The cosine function (cos) is an even function, which means that cos(-x) = cos(x) for all values of x. This property arises from the evenness of the cosine’s graph about the y-axis. On the other hand, the sine function (sin) is an odd function, denoted by sin(-x) = -sin(x). This can be observed from the symmetry of the sine’s graph about the origin.
Another important even odd trig identity involves the tangent function (tan). The tangent function is odd, meaning tan(-x) = -tan(x). The reason behind this property lies in the periodicity of the tangent function, as it repeats itself every π radians.
The reciprocal trigonometric functions, secant (sec), cosecant (csc), and cotangent (cot), also possess even odd properties. The secant function is even (sec(-x) = sec(x)), while the cosecant and cotangent functions are odd (csc(-x) = -csc(x) and cot(-x) = -cot(x), respectively). These properties can be deduced from the definitions of these functions in terms of cosine, sine, and tangent.
Trigonometric Even-odd Functions
Trigonometric functions can be classified as even, odd, or neither based on their symmetry properties. Even functions exhibit symmetry about the y-axis, meaning that if you reflect their graph across the y-axis, you get the same function. Odd functions, on the other hand, have symmetry about the origin, such that reflecting their graph across the origin results in the same function.
Cosine (cos) is a prominent even function in trigonometry. When you plot the cosine function, it appears symmetric about the y-axis, and thus, cos(-x) = cos(x) for all x. This property is expressed in the evenness property of cosine, making it an even function.
Sine (sin), as mentioned earlier, is an odd function. Its graph is symmetric about the origin, and therefore, sin(-x) = -sin(x) for all x. This characteristic is a result of the oddness property of sine.
Tangent (tan), cotangent (cot), secant (sec), and cosecant (csc) are neither even nor odd functions. Their graphs do not exhibit the symmetry properties seen in even and odd functions. For example, the tangent function is neither symmetric about the y-axis nor the origin, and so, tan(-x) is not equal to -tan(x).
In summary, understanding whether a trigonometric function is even, odd, or neither can aid in simplifying trigonometric expressions and solving equations, as it allows for the exploitation of these unique symmetry properties.
Even and Odd Trig Functions with Examples
Trigonometric functions can be classified as even, odd, or neither, based on their symmetry properties. An even function satisfies the condition f(-x) = f(x), while an odd function satisfies f(-x) = -f(x).
Let’s explore some examples of even and odd trig functions with their respective properties.
1: Cosine (cos)
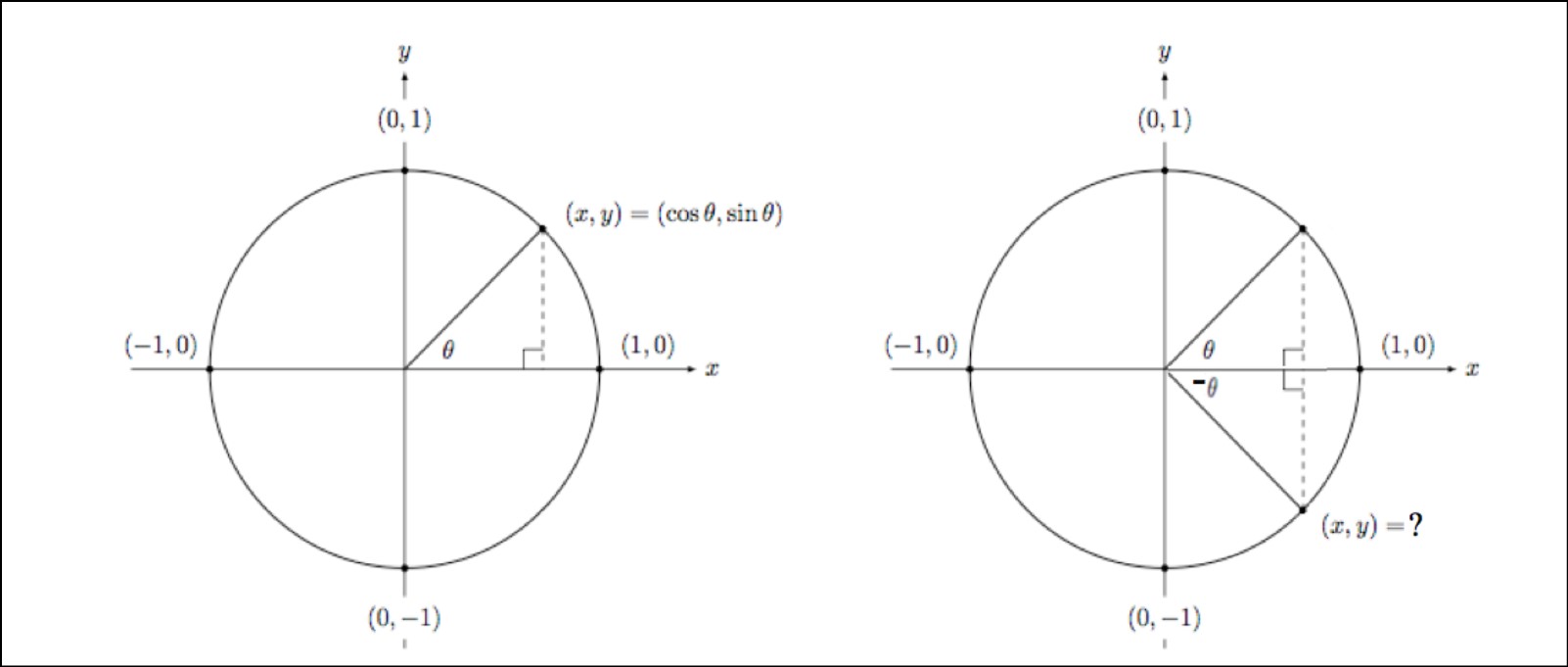
Cosine is an even function. Its graph is symmetric about the y-axis, which means cos(-x) = cos(x) for all x. In terms of the unit circle, the cosine function gives the x-coordinate of a point, and since the unit circle is symmetric about the y-axis, the cosine values remain the same when x is replaced by -x.
2: Sine (sin)
Sine is an odd function. Its graph is symmetric about the origin, so sin(-x) = -sin(x) for all x. In the unit circle, the sine function gives the y-coordinate of a point. Since the unit circle is symmetric about the origin, the sine values change sign when x is replaced by -x.
3: Tangent (tan)
Tangent is neither an even nor an odd function. Its graph does not exhibit symmetry about the y-axis or the origin. Hence, tan(-x) is not equal to -tan(x) for all x.
4: Cotangent (cot)
Cotangent is neither even nor odd. It also lacks the required symmetry properties. Hence, cot(-x) is not equal to -cot(x) for all x.
5: Secant (sec) and Cosecant (csc)
Similar to tangent and cotangent, secant and cosecant are neither even nor odd functions. Their graphs do not demonstrate the expected symmetries, so sec(-x) is not equal to sec(x) and csc(-x) is not equal to -csc(x) for all x.
Understanding whether a trigonometric function is even, odd, or neither helps in simplifying trigonometric expressions, evaluating integrals, and solving various trigonometric equations. Utilizing these properties can lead to more efficient mathematical calculations.