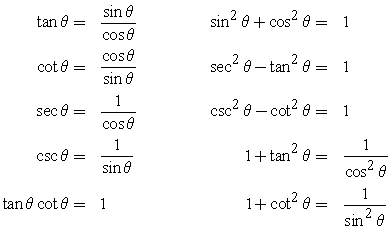Basic Trigonometric Ratios Formula

Trigonometric Ratios: In mathematics, trigonometry is that branch of study, which helps a student to learn about triangles. A student should note that triangles are made out of right angles. From this, basic trigonometric ratios are found. There are six basic trigonometric ratios that are evaluated from the sides of a right-angled triangle.

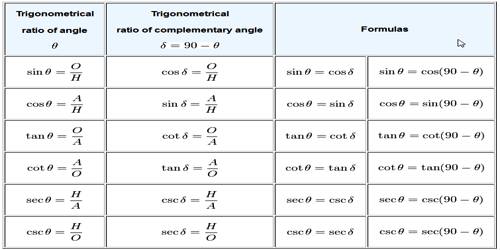
Trigonometric Ratios of Complementary Angles

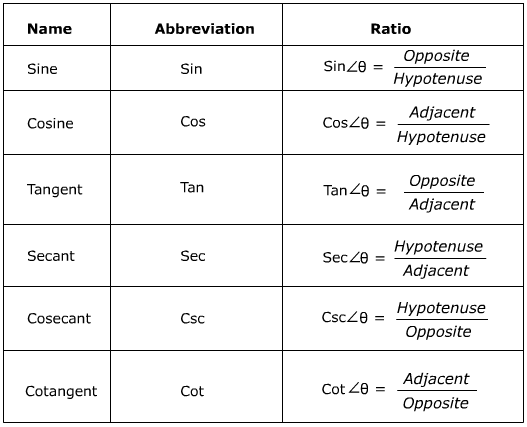
Trigonometric Ratios

Based on the value of the ratio of the sides in a right-angled triangle, trigonometric ratios are defined as the values of all the trigonometric functions. It can be said that the ratios of the sides with respect to any of its acute angles, represent the trigonometric ratio of that specific angle.

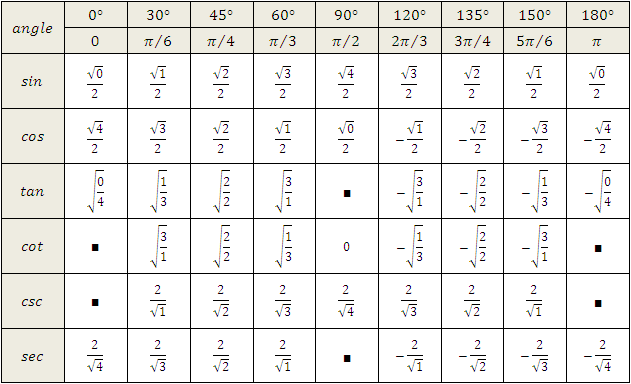
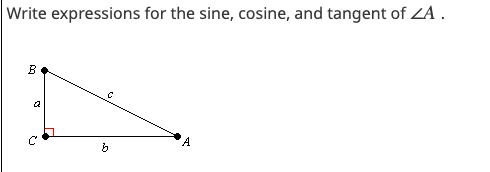
Referring to the above figure, it may be seen it is a right-angled triangle, and at B, it is right angled. Trigonometric ratios are evaluated from the sides of the above right-angled triangle, and are six in numbers. The ratios are listed as sine, cosine, tangent, cotangent, cosecant, and secant. The student will be able to learn to make a table of trigonometry for these ratios with respect to specific angles like 90°,60 °, 45 °,30 ° and 0 °. The trigonometric ratios with respect to angle C are defined below:

Sine of an angle is represented as the ratio of the perpendicular side AB to the angle hypotenuse AC. Cosine of an angle is represented as the ratio of the side adjacent to side BC, to that angle to the hypotenuse AC. Tangent of an angle is represented as ratio of the perpendicular side AB, to that angle, of the side adjacent to that angle.

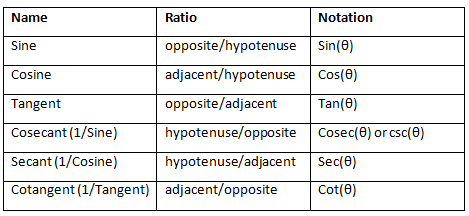
Six Trigonometric Ratios

Cosecant of an angle is defined as the multiplicative inverse of sine. The cotangent of an angle is represented as multiplicative inverse of the tangent. The secant of an angle is represented as a multiplicative inverse of cosine.