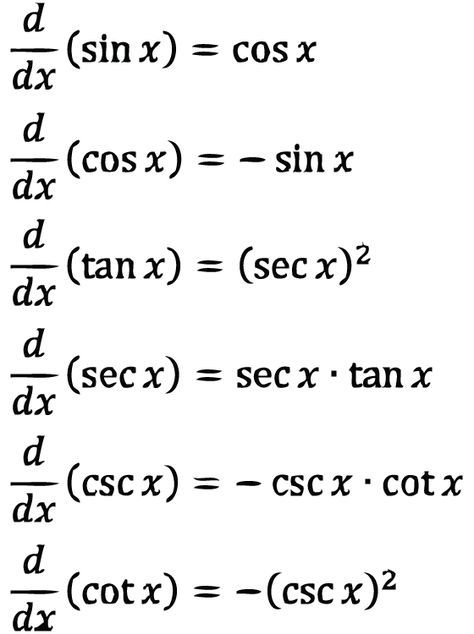Before understanding what Trigonometric Derivatives are, it is essential for a student to know what is meant by the derivative of a function. As a part of one of the fundamental concepts of mathematics, derivative occupies an important place. In calculus, students should know about the process of integration as well as the differentiation of a function. The procedure used for finding the derivative of a function is known as differentiation. Integration is considered as the inverse procedure of differentiation and is known as integration.
- Integration Formula
- Formula of Trigonometry
- Trig Identities
- Trigonometric Ratios
- Trigonometric functions with Formulas
- Heights and distance
- Trigonometry formula Involving Sum Difference Product Identities
- Pythagorean Theorem
- Differentiation Formula
- Basic Trig Identities
Trigonometric Derivatives
Coming to the question of what are trigonometric derivatives and what are they, the derivatives of trigonometric functions involve six numbers. They are cosecant (cscx), secant (secx), cotangent(cotx), tangent(tanx), cosine (cosx), and sine (sinx). These functions can be subjected to the process of differentiation and their corresponding derivatives can be found. These are known as continuous functions. It is possible to find the derivative of trigonometric function through the process of differentiation. With respect to the rate at which a variable can be changed is also referred to as the process of differentiation.
It is possible to show from the first principles that derivatives of tangent, cosine, and sine functions are given as d(tanx)/dx=sec2x, d(cosx)/dx=sinx, and d(sinx)/dx=cosx. The derivative of a trigonometric function can be found by using algebra. At any given value of x and from the general expression of the slope of a curve, it is possible for a student to differentiate a function. This will enable to find the derivative of the particular function in question.
The student should know that there are derivatives of circular trigonometric functions. It can be evaluated through the usage of cos(x) and sin(x). Here, a rule of quotient is applied in order to differentiate the function. The expression that results from this process, leads to the corresponding derivatives of trigonometry.
Derivatives of Inverse Trigonometric Functions
