Master Trigonometry and become a pro at Trig Quadrants! By understanding the relationship between angles and coordinates. You can unlock the ability to solve complex equations with ease. Join us and explore the fascinating world of Trigonometry today!
Trig Quadrants
A trigonometric function is a mathematical function that is used to define relationships between the angles and sides of a right triangle.
In trigonometry, the unit circle is divided into four quadrants, each containing a different sign for sine, cosine, and tangent. The signs of these functions can be used to determine the quadrant in which an angle lies. The quadrants provide a way to reference the position of angles in the coordinate plane.
Angle Quadrants Trigonometry
There are six different trigonometric functions: sine (sin), cosine (cos), tangent (tan), cosecant (csc), secant (sec), and cotangent (cot). These functions are defined in terms of the ratios of the sides of a right triangle and are used to solve problems in various fields such as mathematics, engineering, physics, and astronomy.
In this article, we will focus on the concept of trigonometric quadrants and their role in the study of trigonometry.
The unit circle is a circle with a radius of one unit and is used to define the values of the trigonometric functions. Unit circle is divided into four regions called quadrants, which are defined by the x- and y-axes. The x-axis and y-axis divide the unit circle into four equal parts. Each representing 90 degrees or one-quarter of a full circle.
Trig Quadrants – Trigonometry Quadrants
Each of the four quadrants is associated with a unique set of values for the trigonometric functions.
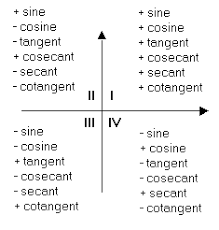
- In the first quadrant, which is located in the upper right part of the unit circle, all the values of the trigonometric functions are positive.
- In the second quadrant, which is located in the upper left part of the unit circle, the values of the sine function are positive and the values of the cosine function are negative.
- The third quadrant, which is located in the lower left part of the unit circle, all the values of the trigonometric functions are negative.
- In the fourth quadrant, which is located in the lower right part of the unit circle, the values of the sine function are negative and the values of the cosine function are positive.
The sine function is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse. Cosine function is defined as the ratio of the length of the side adjacent to the angle to the length of the hypotenuse. The tangent function is defined as the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
Trigonometry and Quadrants
The values of the trigonometric functions in each of the four quadrants can be determined using the unit circle. For example,
- In the first quadrant, the sine function is positive. That means that the length of the side opposite the angle is greater than the length of the side adjacent to the angle.
- The second quadrant, the cosine function is negative. That means that the length of the side adjacent to the angle is negative.
- In the third quadrant, both the sine and cosine functions are negative, which means that both the length of the side opposite the angle and the length of the side adjacent to the angle are negative.
- The fourth quadrant, the sine function is negative and the cosine function is positive, which means that the length of the side opposite the angle is negative and the length of the side adjacent to the angle is positive.
The tangent function is also used in each of the four quadrants to determine the value of the side opposite the angle and the side adjacent to the angle. The values of the tangent function in each of the four quadrants are determined by the values of the sine and cosine functions. In the first quadrant, the tangent function is positive. That means that the length of the side opposite the angle is greater than the length of the side adjacent to the angle.

