Understanding How to Find Trigonometric Ratios is essential for solving various mathematical problems involving angles and sides of triangles. Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. The three primary trigonometric ratios – sine, cosine, and tangent – play a crucial role in many real-world applications, such as engineering, physics, and navigation.
In this guide, we will walk you through the process of finding trigonometric ratios with clear explanations and illustrative examples, making it easier for you to grasp and apply these concepts confidently.
How to Find Trigonometric Ratios
Trigonometric ratios are essential mathematical tools used to establish relationships between the angles and sides of a right triangle. The three primary trigonometric ratios are sine (sin), cosine (cos), and tangent (tan).
To find these ratios, you need to follow these steps:
- Understand the Triangle. Make sure you have a right triangle, which means one of the angles is 90 degrees (a right angle). Identify the angle you are interested in measuring.
- Identify the Sides. Label the sides of the triangle relative to the chosen angle. The side opposite the angle is the opposite side (O), the side adjacent to the angle is the adjacent side (A), and the side opposite the right angle (the hypotenuse) is H.
- Choose the Ratio. Based on the angle you want to evaluate, select the appropriate trigonometric ratio. For example, if you want to find the sine of the angle, use sin = O/H; for cosine, use cos = A/H; and for tangent, use tan = O/A.
- Calculate the Ratio. Divide the length of the side corresponding to the selected ratio by the length of the hypotenuse to find the trigonometric ratio.
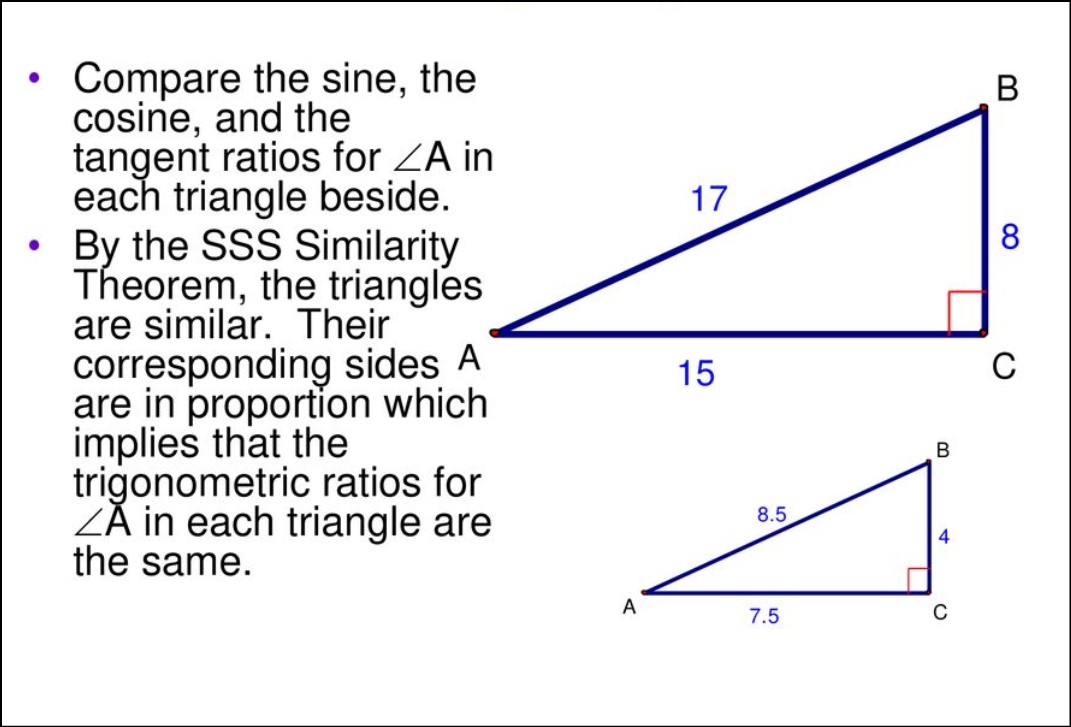
Keep in mind that trigonometric ratios only depend on the angle, not the size of the triangle. Therefore, the ratios remain the same for similar triangles with different dimensions. Learn How to Find Angle In Trigonometry
What Are Trigonometric Ratios
Trigonometric ratios are fundamental mathematical concepts used in trigonometry to relate the angles of a right triangle to the lengths of its sides. In a right triangle, which contains a 90-degree angle, there are three primary trigonometric ratios: sine (sin), cosine (cos), and tangent (tan).
The sine of an angle is the ratio of the length of the side opposite the angle to the length of the hypotenuse. The cosine of an angle is the ratio of the length of the side adjacent to the angle to the length of the hypotenuse. The tangent of an angle is the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
Trigonometric ratios have numerous real-world applications. Especially in fields such as engineering, physics, architecture, and astronomy. They used to solve various problems involving angles and distances, such as calculating the height of buildings. Determining the distance of objects, and analyzing the motion of objects in space.
These ratios have a range of values between -1 and 1, where -1 signifies the maximum negative value. 0 represents a right angle, and 1 denotes the maximum positive value. They fundamental to trigonometric functions and play a pivotal role. In various mathematical concepts and calculations.
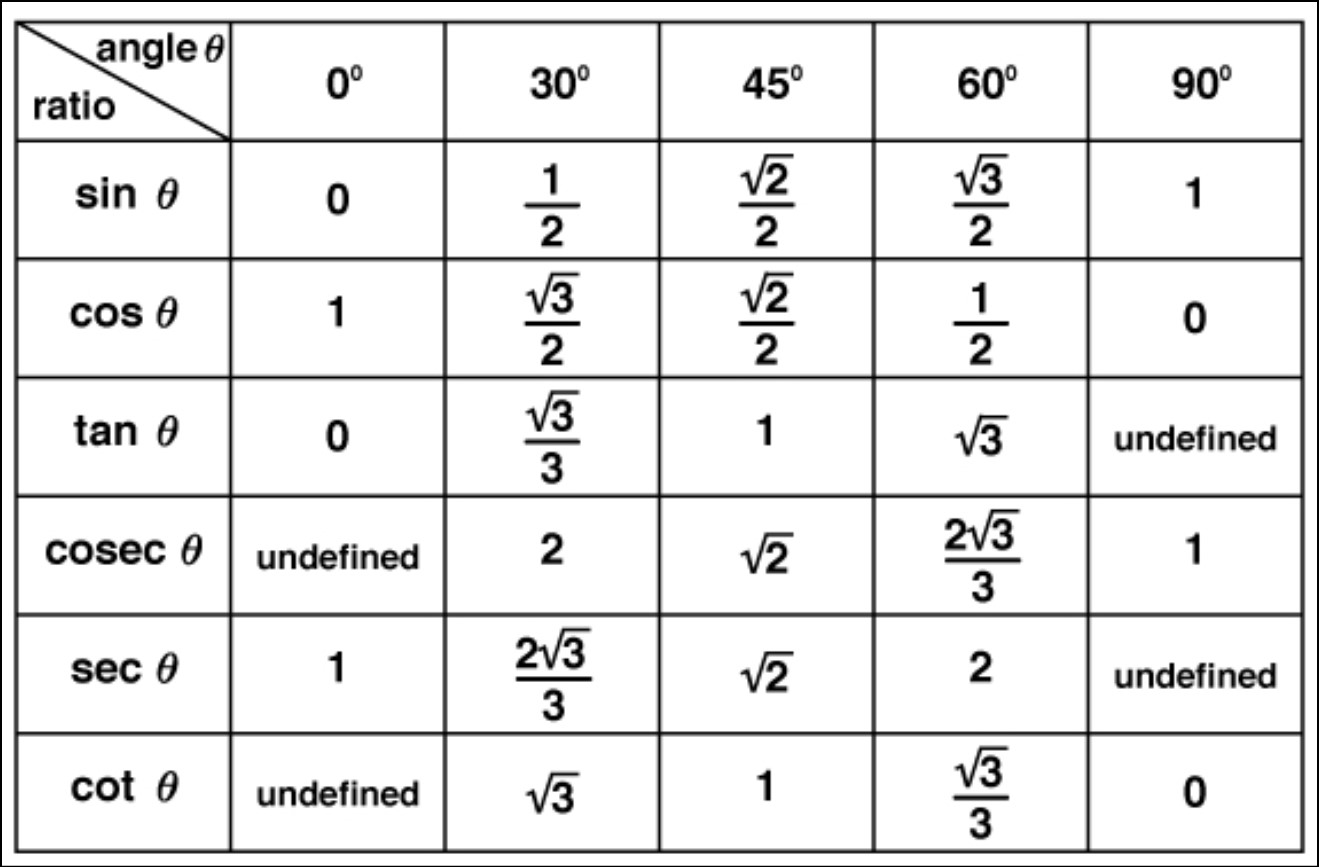
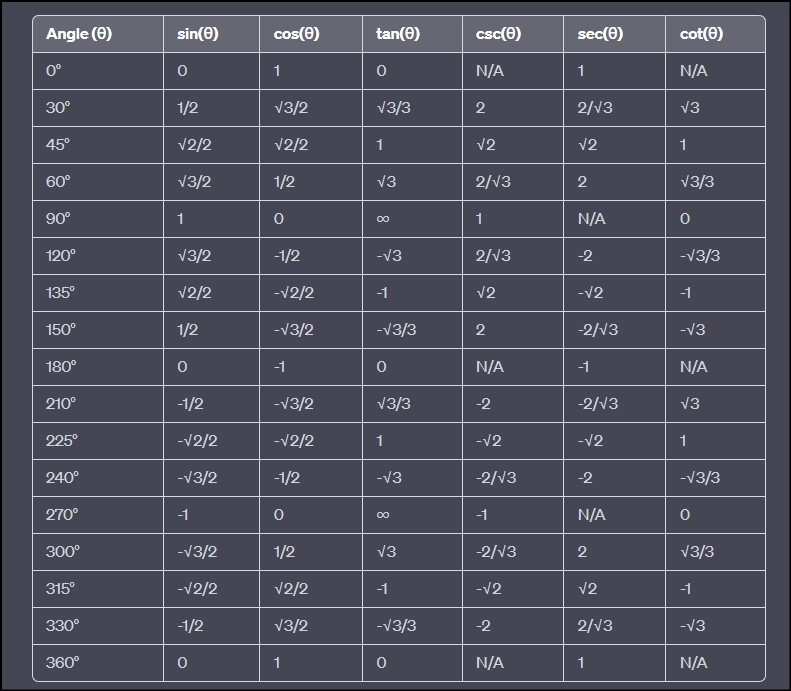
Table for Trigonometric Ratios
Trigonometric ratios, conveniently presented in tables for quick reference and ease of use. These tables list the values of sine, cosine, and tangent for different angles within a right triangle. Since the ratios dependent on the angle, these tables help in rapidly obtaining the ratios without the need for complex calculations.
The table for trigonometric ratios typically includes common angles such as 0°, 30°, 45°, 60°, and 90°, as well as their corresponding ratios. For example, the sine of 30° is 0.5, the cosine of 45° is 0.707, and the tangent of 60° is √3 (approximately 1.732).
Modern calculators and mathematical software also incorporate trigonometric functions, making it easier to calculate ratios for any angle. However, understanding these tables is essential as it provides a foundational understanding of the relationship between angles and their corresponding trigonometric values.
By using trigonometric tables, students, engineers, and scientists can quickly determine trigonometric ratios without the need for a calculator, which proves beneficial in exams and problem-solving situations where a quick reference is needed
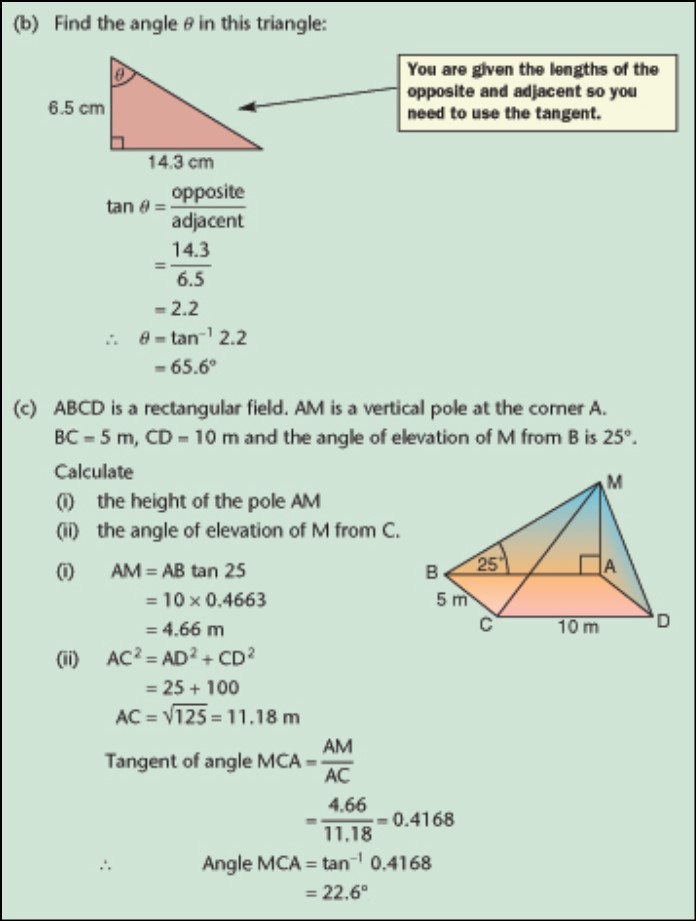
Trigonometric Ratios Examples
Trigonometric ratios find practical application in various scenarios, and understanding their use through examples can insightful.
Here are some examples:
- Finding Height. Imagine you have a ladder leaning against a wall forming a right triangle. The angle of elevation to the top of the wall is 60°, and the ladder’s length is 5 meters. By using the tangent ratio (tan = Opposite/Adjacent), you can find the wall’s height (opposite side). Height = 5 meters * tan(60°) ≈ 8.66 meters.
- Projectile Motion. In physics, you can analyze the trajectory of a projectile using trigonometric ratios. For instance, the horizontal distance traveled by a ball launched at an angle of 45° with a velocity of 20 m/s can calculated using cosine (cos = Adjacent/Hypotenuse). Distance = 20 m/s * cos(45°) ≈ 14.14 meters.
- Surveying Land. Trigonometric ratios valuable in land surveying to measure distances and angles between points. By measuring angles and using trigonometry, surveyors can calculate the distance between inaccessible points.
- Astronomy. In astronomy, trigonometric ratios help measure distances to celestial objects. By observing the angle of a celestial body from two different locations on Earth, astronomers can use trigonometry to determine the object’s distance from Earth.
These examples highlight the practical significance of trigonometric ratios in various fields. And demonstrate their ability to solve real-world problems involving angles, distances, and heights. Understanding trigonometric ratios allows individuals to tackle a wide range of challenges and make accurate calculations in different applications.