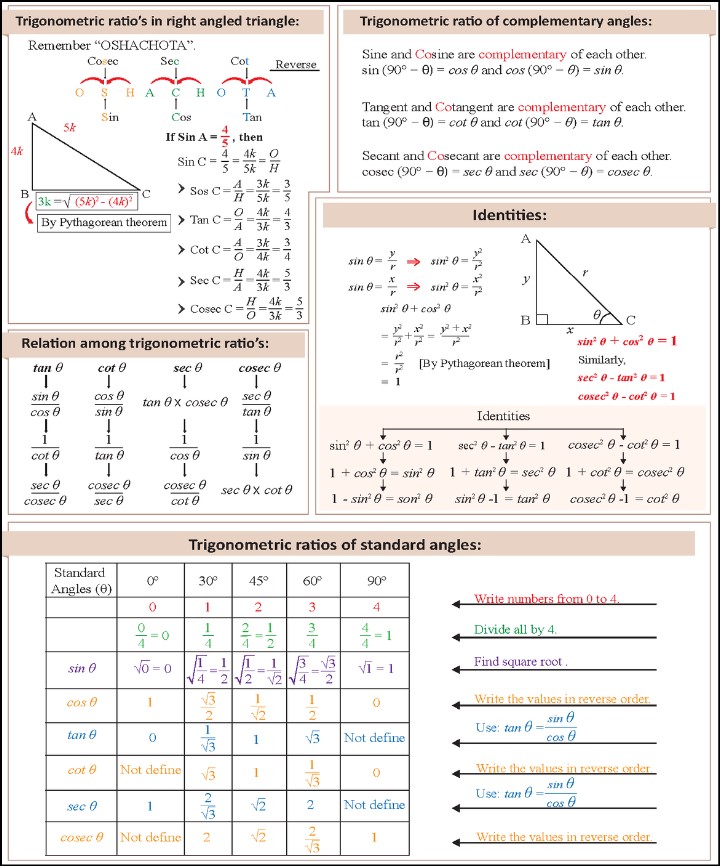
Trig Identities Cheat Sheet
Trigonometric identities are essential tools in the study of trigonometry, enabling us to simplify complex expressions and solve various problems.

This trig identities cheat sheet serves as a handy reference to the most commonly used identities:
1. Pythagorean Identities:
- Sin²θ + Cos²θ = 1: This identity is derived from the Pythagorean theorem and connects the sine and cosine functions.
- 1 + Tan²θ = Sec²θ and 1 + Cot²θ = Csc²θ: These identities relate the tangent and cotangent functions with secant and cosecant functions, respectively.
2. Reciprocal Identities:
- Cscθ = 1 / Sinθ, Secθ = 1 / Cosθ, and Cotθ = 1 / Tanθ: These identities express cosecant, secant, and cotangent functions in terms of their reciprocal trig functions.
3. Quotient Identities:
- Tanθ = Sinθ / Cosθ and Cotθ = Cosθ / Sinθ: These identities relate tangent and cotangent to sine and cosine functions, respectively.
4. Co-Function Identities:
- Sin(π/2 – θ) = Cosθ, Cos(π/2 – θ) = Sinθ, Tan(π/2 – θ) = Cotθ: These identities define the relationships between trigonometric functions and their complementary angles.
5. Double Angle Identities:
- Sin(2θ) = 2 * Sinθ * Cosθ, Cos(2θ) = Cos²θ – Sin²θ, Tan(2θ) = 2 * Tanθ / (1 – Tan²θ): These identities are useful for simplifying expressions with double angles.
6. Sum and Difference Identities:
- Sin(θ ± φ) = Sinθ * Cosφ ± Cosθ * Sinφ, Cos(θ ± φ) = Cosθ * Cosφ ∓ Sinθ * Sinφ: These identities allow us to express the sine and cosine of the sum or difference of two angles.
7. Half Angle Identities:
- Sin(θ/2) = ± √[(1 – Cosθ) / 2], Cos(θ/2) = ± √[(1 + Cosθ) / 2], Tan(θ/2) = ± √[(1 – Cosθ) / (1 + Cosθ)]: These identities are helpful when dealing with half angles.
Trigonometric Identities Cheat Sheet
Trigonometric identities are fundamental equations that establish relationships between various trigonometric functions. Having a comprehensive cheat sheet can be immensely helpful in simplifying expressions, solving equations, and understanding the properties of trigonometric functions.
Below are some essential trigonometric identities:
1. Pythagorean Identities:
- Sin²θ + Cos²θ = 1
- 1 + Tan²θ = Sec²θ
- 1 + Cot²θ = Csc²θ
2. Reciprocal Identities:
- Cscθ = 1 / Sinθ
- Secθ = 1 / Cosθ
- Cotθ = 1 / Tanθ
3. Quotient Identities:
- Tanθ = Sinθ / Cosθ
- Cotθ = Cosθ / Sinθ
4. Co-Function Identities:
- Sin(π/2 – θ) = Cosθ
- Cos(π/2 – θ) = Sinθ
- Tan(π/2 – θ) = Cotθ
5. Double Angle Identities:
- Sin(2θ) = 2 * Sinθ * Cosθ
- Cos(2θ) = Cos²θ – Sin²θ
- Tan(2θ) = 2 * Tanθ / (1 – Tan²θ)
6. Sum and Difference Identities:
- Sin(θ ± φ) = Sinθ * Cosφ ± Cosθ * Sinφ
- Cos(θ ± φ) = Cosθ * Cosφ ∓ Sinθ * Sinφ
7. Half Angle Identities:
- Sin(θ/2) = ± √[(1 – Cosθ) / 2]
- Cos(θ/2) = ± √[(1 + Cosθ) / 2]
- Tan(θ/2) = ± √[(1 – Cosθ) / (1 + Cosθ)]
Understanding and memorizing these trigonometric identities will significantly simplify your trigonometry problem-solving and boost your confidence in dealing with various trigonometric expressions and equations. Always verify the conditions under which these identities are valid and practice applying them in different scenarios to reinforce your understanding.
Solving Trigonometric Proofs Cheat Sheet
Solving trigonometric proofs can be a challenging task, requiring a deep understanding of trigonometric identities and algebraic manipulation.
This cheat sheet provides a step-by-step approach to tackle trigonometric proofs effectively:
1. Start with One Side:
- When dealing with an equation involving trigonometric functions, it’s often helpful to choose the more complex side or the side you wish to simplify.
2. Identify Known Identities:
- Refer to the Trigonometric Identities Cheat Sheet and identify relevant trigonometric identities that can help simplify the side you chose.
3. Apply Trigonometric Identities:
- Utilize the identified identities to simplify the chosen side of the equation. Be careful with algebraic manipulation and ensure that you apply the identities correctly.
4. Work with Both Sides:
- Perform the same steps (applying identities and algebraic manipulation) on the other side of the equation, trying to get it into a form that matches the simplified side.
5. Use Equalities:
- If you reach a point where both sides of the equation match, use the transitive property of equality to show that the original equation holds.
6. Verify Domain Restrictions:
- Some trigonometric identities have domain restrictions, such as excluding values that cause division by zero. Make sure to verify that the solutions obtained are within the permissible domain.
7. Check for Extraneous Solutions:
- At times, during the simplification process, extraneous solutions may be introduced. Verify that the solutions obtained satisfy the original equation.
8. Practice and Patience:
- Solving trigonometric proofs requires practice and patience. Work through various examples, and don’t be discouraged by initial challenges. As you become more familiar with the identities and techniques, solving trigonometric proofs will become more manageable.
By following this systematic approach and becoming proficient with trigonometric identities, you’ll enhance your ability to tackle complex proofs, making trigonometry a more rewarding and enjoyable subject.