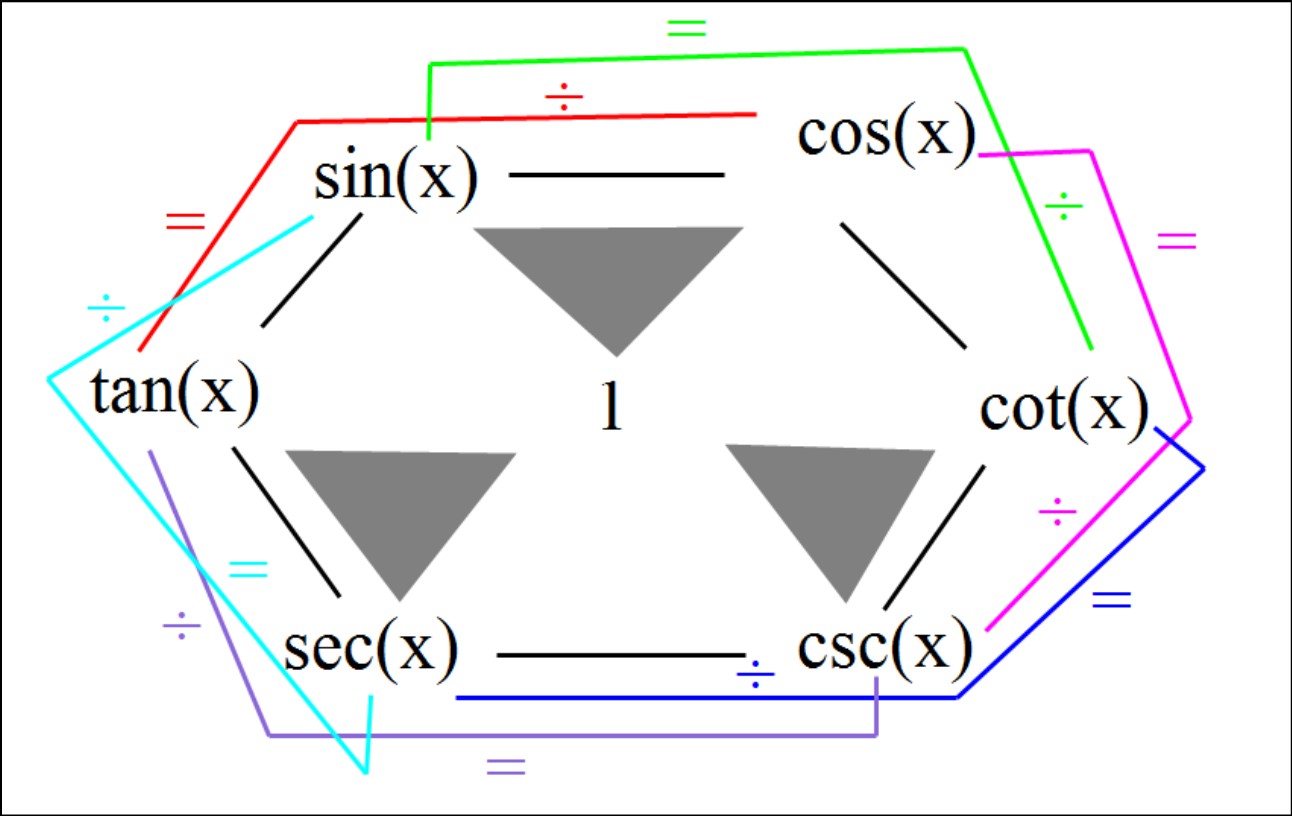
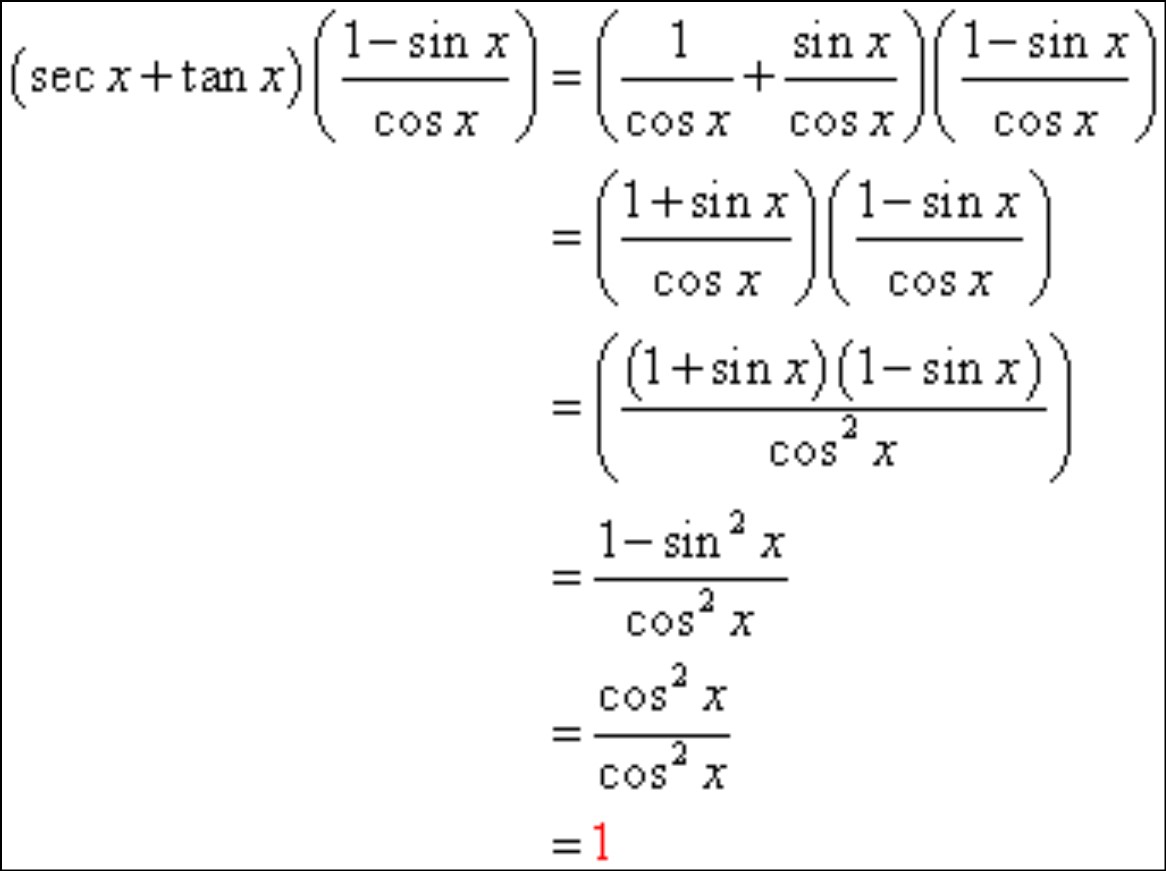How to Verify Trig Identities: Trigonometric identities play a crucial role in simplifying complex trigonometric expressions and solving various mathematical problems. However, verifying these identities can often be a challenging task, especially for those new to trigonometry.
In this article, we will present you with easy-to-follow methods and step-by-step instructions to verify trig identities effortlessly. Whether you’re a student struggling with trigonometry or someone seeking a quick refresher, our straightforward techniques will help you gain confidence in tackling these identities with ease. Let’s dive in and demystify the process of verifying trig identities.
How to Verify Trig Identities
Verifying trigonometric identities is an essential skill in trigonometry. It involves confirming that an equation is true for all values of the variables involved. While it may seem daunting at first, with a systematic approach and some useful tips, you can master this process.
Here’s a step-by-step guide to verify trig identities effectively:
Step 1: Know the Fundamental Identities
Before attempting to verify any trigonometric identity, ensure you are familiar with the fundamental trigonometric identities. These include Pythagorean identities, reciprocal identities, quotient identities, and cofunction identities. Being well-versed in these will serve as a solid foundation for verifying more complex identities.
Step 2: Simplify Both Sides of the Equation
Start by simplifying each side of the equation independently. Utilize trigonometric identities, algebraic techniques, and basic trigonometric relationships to simplify expressions. Aim to make both sides of the equation look as similar as possible.
Step 3: Transform One Side to Match the Other
Use algebraic manipulation and trigonometric identities to transform one side of the equation so that it matches the other side. Your goal is to reach a point where both sides are precisely equal to each other.
Step 4: Verify for All Values
Once you have transformed one side to match the other, the final step is to verify the identity for all possible values of the variables involved. This usually involves substituting various angles or trigonometric values to ensure the equation holds true universally.
Remember, patience and practice are key to becoming proficient in verifying trig identities. Work through numerous examples to reinforce your understanding and sharpen your skills. Learn more:- How to Graph a Trig Function with Chart
How to Memorize Trigonometry Identities
Memorizing trigonometric identities can be a challenging task, but it is essential to save time and enhance problem-solving in trigonometry.
Instead of rote memorization, try these effective techniques to make the process more manageable and enjoyable:
Visual Aids and Mnemonics
Use visual aids, such as unit circles, right triangles, or graphs, to visualize the trigonometric functions and their relationships. Additionally, create mnemonics or acronyms to help recall the identities easily. For example, SOH-CAH-TOA for sine, cosine, and tangent in a right triangle.
Group Similar Identities
Organize trigonometric identities into groups based on their types, such as Pythagorean identities, double-angle identities, or half-angle identities. Recognizing patterns within each group can make memorization more systematic.
Use Trigonometric Ratios
Understand the trigonometric ratios in a right triangle: sine, cosine, and tangent. From there, derive other trigonometric identities using these fundamental ratios. This approach creates a logical connection between different identities.
Practice with Flashcards and Repetition
Create flashcards with one side showing an identity and the other side showing the corresponding formula. Regularly review these flashcards to reinforce your memory. Repetition is crucial for long-term retention.
How To Prove Trig Identities
Proving trigonometric identities involves showing that one side of the equation can be transformed into the other side using a series of mathematical steps. This process requires a combination of algebraic skills and knowledge of trigonometric properties.
Follow these steps to prove trig identities convincingly:
Step 1: Analyze the Problem
Start by carefully analyzing the identity you need to prove. Identify the specific trigonometric functions involved and any patterns or relationships that might be applicable.
Step 2: Utilize Fundamental Identities
Use the fundamental trigonometric identities as building blocks for your proof. These identities can be found in any trigonometry textbook or reference material.
Step 3: Work on One Side at a Time
It’s often best to focus on one side of the equation at a time. Begin with the more complex-looking side or the one that has the least number of terms.
Step 4: Transform Both Sides Equally
As you make progress on one side, aim to transform the other side in the same manner. The goal is to make both sides look identical or equal to each other.
Step 5: Show Equivalence
At this stage, you should have both sides of the equation in the same form. To complete the proof, explicitly state that both sides are equivalent or equal to each other, making sure to account for all steps and transformations made.
Step 6: Verify for All Values
For a complete proof, verify that the identity holds true for all values of the variables involved. This may involve substituting various angles or trigonometric values into the equation.
In conclusion, proving trig identities is a challenging yet rewarding exercise that strengthens your understanding of trigonometry and improves your problem-solving skills. With patience and practice, you’ll become more proficient in tackling even the most complex identities.