Trigonometry Quadrant: In trigonometry, the unit circle is often used to define the values of trigonometric functions such as sine, cosine, and tangent. The unit circle is a circle with a radius of 1 and its center at the origin of a coordinate plane.
Trigonometry Quadrant
In trigonometry, the concept of a quadrant is crucial for understanding the behavior and properties of angles within the Cartesian coordinate plane. The Cartesian coordinate plane is divided into four quadrants, labeled as the first quadrant, second quadrant, third quadrant, and fourth quadrant. Each quadrant is defined by the signs of the x and y coordinates, allowing us to classify angles based on their position within the plane.
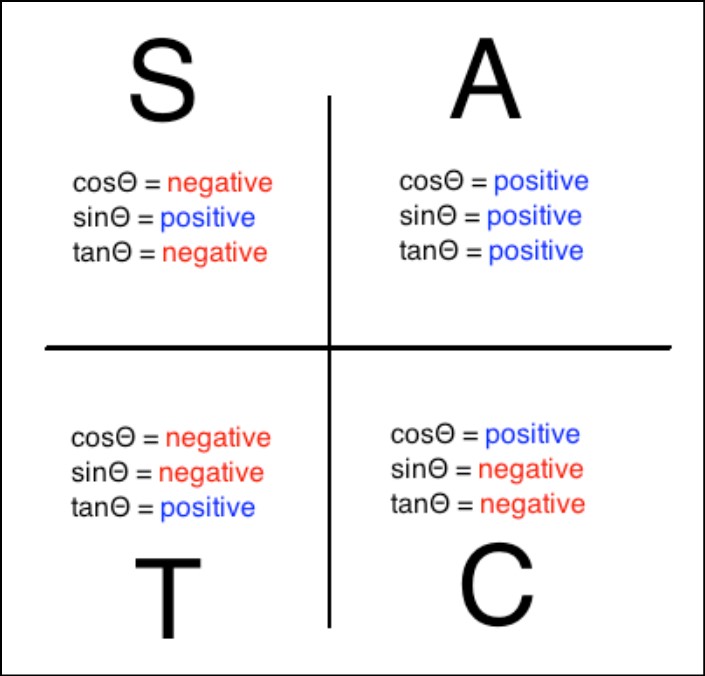
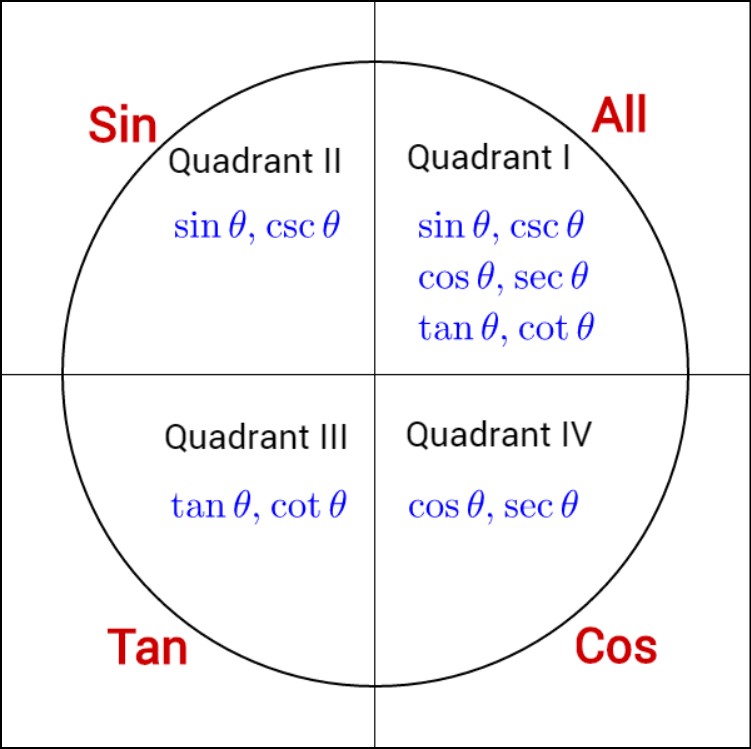
The first quadrant is located in the upper right portion of the coordinate plane. In this quadrant, both the x and y coordinates are positive. Angles within the first quadrant range from 0 to 90 degrees (or 0 to π/2 radians). Trigonometric functions such as sine, cosine, and tangent are positive in this quadrant.
Moving counterclockwise from the first quadrant, we reach the second quadrant. In the second quadrant, the x coordinate is negative while the y coordinate remains positive. Angles in the second quadrant range from 90 to 180 degrees (or π/2 to π radians). In this quadrant, only the sine function is positive, while the cosine and tangent functions become negative.
Continuing counterclockwise, we come to the third quadrant. Here, both the x and y coordinates are negative. The third quadrant covers angles ranging from 180 to 270 degrees (or π to 3π/2 radians). In this quadrant, only the tangent function is positive, while the sine and cosine functions are negative.
Finally, the fourth quadrant is located in the lower right portion of the coordinate plane. In the fourth quadrant, the x coordinate is positive, while the y coordinate is negative. Angles in this quadrant range from 270 to 360 degrees (or 3π/2 to 2π radians). In the fourth quadrant, only the cosine function is positive, while the sine and tangent functions become negative.
Finding Quadrants of Trigonometry
Determining the quadrant of a given angle is an essential skill in trigonometry. It allows us to understand the properties and behavior of angles based on their position in the coordinate plane. To find the quadrant of a given angle, we need to examine its measure and compare it to the ranges covered by each quadrant.
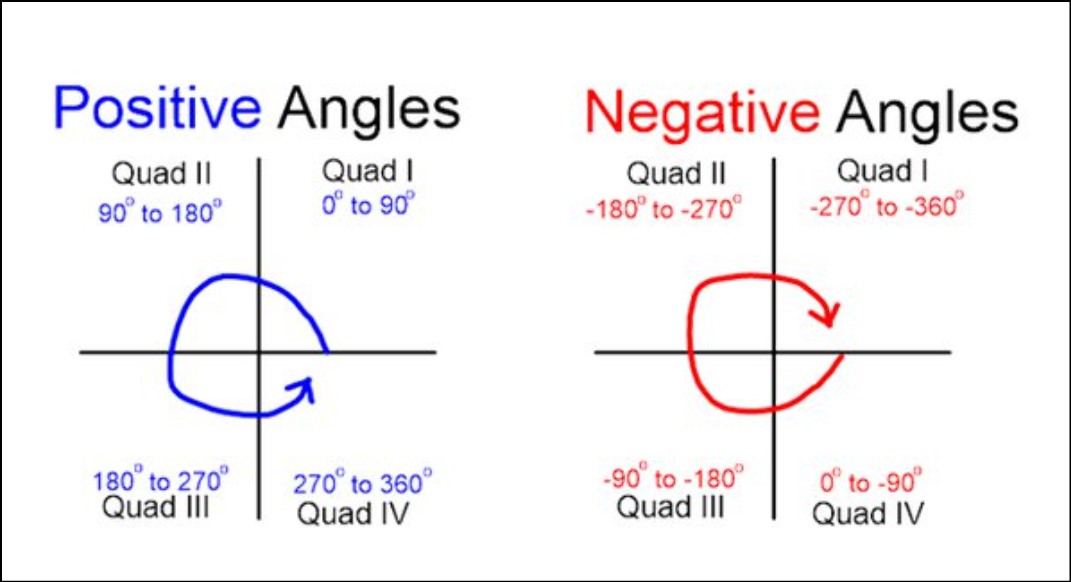
Suppose we have an angle in standard position, which means its initial side coincides with the positive x-axis. If the angle measures between 0 and 90 degrees (or 0 and π/2 radians), it falls in the first quadrant. This is because the first quadrant covers angles where both the x and y coordinates are positive.
If the angle measures between 90 and 180 degrees (or π/2 and π radians), it belongs to the second quadrant. In this quadrant, the x-coordinate is negative, while the y-coordinate remains positive.
For angles between 180 and 270 degrees (or π and 3π/2 radians), they fall into the third quadrant. Here, both the x and y coordinates are negative.
Lastly, angles between 270 and 360 degrees (or 3π/2 and 2π radians) lie in the fourth quadrant. In this quadrant, the x-coordinate is positive, while the y-coordinate is negative. Check out other Trig posts:- Trig Substitution Integration, Trigonometry Ratios, Trigonometric Functions.
By analyzing the measure of an angle and comparing it to the ranges of each quadrant, we can easily determine which quadrant it belongs to. This knowledge is crucial for working with trigonometric functions, as it allows us to understand the sign and behavior of these functions based on the quadrant in which the angle lies.
Trigonometry Quadrantal Angles
In trigonometry, the term “quadrantal angles” refers to specific angles that lie on the axes of the Cartesian coordinate plane. These angles have special properties and are easily identifiable due to their position relative to the x and y axes.
The quadrantal angles include 0 degrees (or 0 radians), 90 degrees (or π/2 radians), 180 degrees (or π radians), and 270 degrees (or 3π/2 radians). Each of these angles lies on a different axis: 0 degrees lies on the positive x-axis, 90 degrees on the positive y-axis, 180 degrees on the negative x-axis, and 270 degrees on the negative y-axis.
These quadrantal angles have distinct values for the trigonometric functions. At 0 degrees and 180 degrees, the sine function is 0, while the cosine function is 1 and -1, respectively. At 90 degrees and 270 degrees, the cosine function is 0, while the sine function is 1 and -1, respectively. The tangent function, however, is undefined for these quadrantal angles, as it involves dividing by 0.
Quadrantal angles are significant in trigonometry because they serve as reference points for calculating the values of trigonometric functions and solving various trigonometric equations. Understanding their properties and their relationship to the axes allows us to navigate the complexities of trigonometry with greater ease and accuracy.