Trig Function Identities: Trigonometric function identities play a pivotal role in the study of trigonometry, enabling us to establish valuable relationships between different trigonometric functions. Among these identities, the cofunction and inverse trigonometric function identities hold particular significance. Cofunction identities reveal the complementary nature of certain trigonometric functions, simplifying calculations involving complementary angles.
On the other hand, inverse trigonometric function identities help us find angle measures when given specific trigonometric ratios. Together, these identities expand our understanding of trigonometry and its applications, providing powerful tools for solving complex problems in various fields of mathematics and beyond.
Trig Function Identities
Trigonometric function identities are mathematical relationships that involve trigonometric functions and are true for all valid angles. These identities play a crucial role in simplifying trigonometric expressions, solving equations, and proving other mathematical theorems. The primary trigonometric function identities are the reciprocal, quotient, Pythagorean, and even-odd identities.
The reciprocal identities are based on the reciprocal relationships between trigonometric functions. For any angle θ, the following hold true:
- Cosecant (csc) and Sine (sin) are reciprocal: csc(θ) = 1/sin(θ)
- Secant (sec) and Cosine (cos) are reciprocal: sec(θ) = 1/cos(θ)
- Cotangent (cot) and Tangent (tan) are reciprocal: cot(θ) = 1/tan(θ)
The quotient identities involve the relationships between the trigonometric functions of complementary angles. For any angle θ:
- Tangent (tan) and Cotangent (cot) are reciprocal: tan(θ) = 1/cot(θ)
- Sine (sin) and Cosecant (csc) are reciprocal: sin(θ) = 1/csc(θ)
- Cosine (cos) and Secant (sec) are reciprocal: cos(θ) = 1/sec(θ)
The Pythagorean identities are essential for relating the three main trigonometric functions and are derived from the Pythagorean theorem. For any angle θ:
- sin^2(θ) + cos^2(θ) = 1
- 1 + cot^2(θ) = csc^2(θ)
- tan^2(θ) + 1 = sec^2(θ)
Lastly, the even-odd identities highlight the symmetry properties of trigonometric functions with respect to the origin. For any angle θ:
- sin(-θ) = -sin(θ)
- cos(-θ) = cos(θ)
- tan(-θ) = -tan(θ)
- cot(-θ) = -cot(θ)
Understanding these trigonometric function identities is fundamental for trigonometry and its applications in various fields such as physics, engineering, and computer graphics. Learn more:- Trig Limit Identities
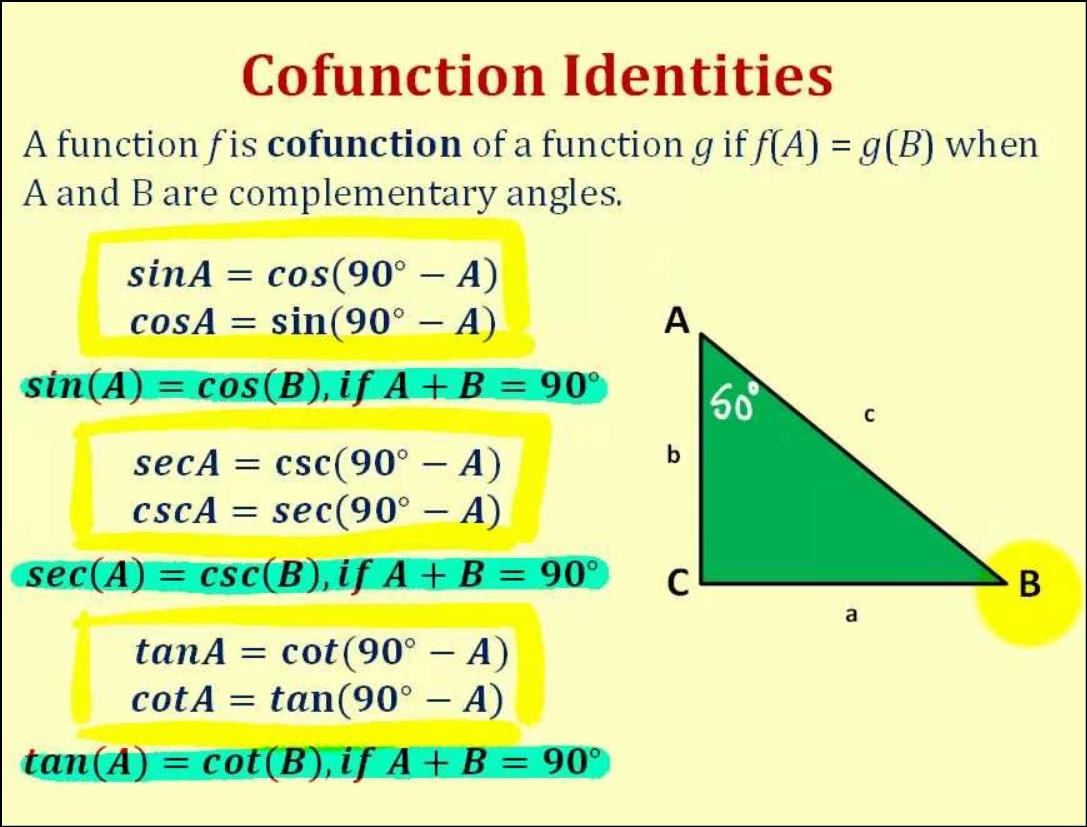
Cofunction Trig Identities
Cofunction trig identities are a set of trigonometric relationships that express the complementary nature of certain trigonometric functions. Complementary angles are two angles whose sum is 90 degrees (π/2 radians). The cofunction identities can be used to simplify trigonometric expressions and equations involving complementary angles.
The first set of cofunction identities is based on the sine and cosine functions:
- sin(π/2 – θ) = cos(θ)
- cos(π/2 – θ) = sin(θ)
These identities show that the sine of an angle is equal to the cosine of its complement, and vice versa.
The second set of cofunction identities involves the tangent and cotangent functions:
- tan(π/2 – θ) = 1/tan(θ)
- cot(π/2 – θ) = 1/cot(θ)
These identities illustrate that the tangent of an angle is equal to the reciprocal of the tangent of its complement, and the same applies to the cotangent function.
Cofunction identities are particularly useful when dealing with right triangles and solving trigonometric equations involving complementary angles. They provide a way to relate trigonometric functions of complementary angles without having to perform additional calculations.
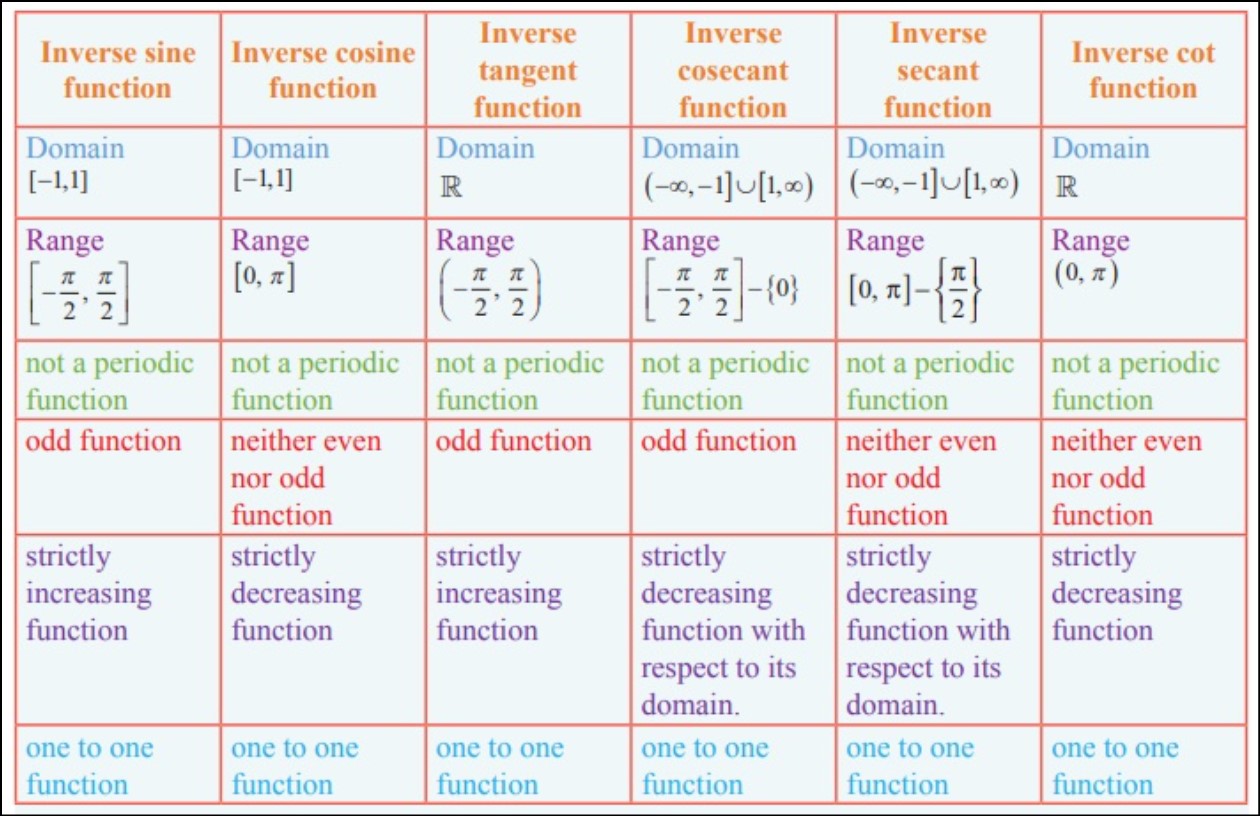
Inverse Trig Function Identities
Inverse trigonometric functions, also known as arc trigonometric functions, are used to find the angle when given the value of a trigonometric ratio. The main inverse trigonometric functions are arcsine (arcsin or sin^-1), arccosine (arccos or cos^-1), and arctangent (arctan or tan^-1).
The identities for inverse trig functions express the relationship between a trigonometric function and its inverse function. For any angle θ:
- sin(arcsin(θ)) = θ
- arcsin(sin(θ)) = θ
These identities demonstrate that applying the arcsine function to a sine value and vice versa “undoes” each other’s effect, resulting in the original angle θ.
Similarly, for cosine:
- cos(arccos(θ)) = θ
- arccos(cos(θ)) = θ
And for tangent:
- tan(arctan(θ)) = θ
- arctan(tan(θ)) = θ
The domain of the inverse trigonometric functions is carefully chosen to ensure a one-to-one correspondence between the trigonometric function and its inverse. This choice allows us to find unique angle solutions within a specific range for inverse trigonometric functions.
Inverse trigonometric function identities are essential when solving trigonometric equations, evaluating integrals involving trigonometric functions, and in various applications of calculus, physics, and engineering where it is necessary to find angle measures based on trigonometric ratios.