Trig Limit Identities: Trigonometry plays a crucial role in various mathematical disciplines, and one of its essential applications in evaluating limits. Trig limit identities powerful tools that allow us to simplify and solve complex trigonometric expressions as they approach specific values. By understanding these identities and mastering the techniques to manipulate them, you can efficiently tackle challenging limit problems involving trigonometric functions.
In this guide, we will explore the fundamental trigonometry identities for limits, equipping you with the knowledge and skills to handle them with confidence. Let’s dive into the world of trigonometry identities and uncover the key insights they offer for limit evaluations.
Trig Limit Identities
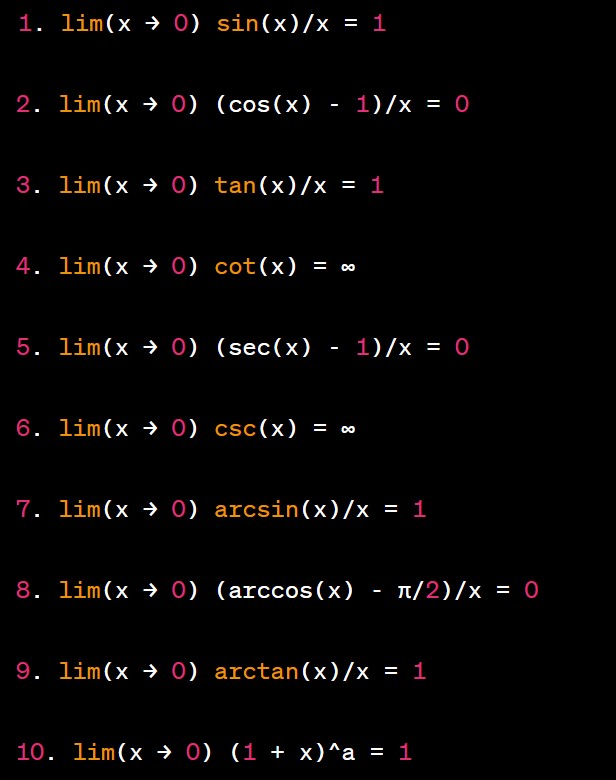
Trig limit identities- fundamental mathematical expressions used to evaluate limits involving trigonometric functions. These identities play a crucial role in calculus and essential for solving complex limits. One of the most commonly used identities the Sine Limit Identity: lim(x → 0) sin(x)/x = 1. This identity forms the basis for many other trigonometric limit calculations. It arises from the geometric interpretation of sine as the ratio of the opposite side to the hypotenuse in a right-angled triangle.
Another important identity the Cosine Limit Identity: lim(x → 0) (cos(x) – 1)/x = 0. This identity derived using the trigonometric addition formula for cosine and often used when evaluating limits involving cosine functions. Together with the Sine Limit Identity, it forms the basis for evaluating more complex trigonometric limits.
Furthermore, the Tangent Limit Identity: lim(x → 0) tan(x)/x = 1, another crucial identity that arises from the ratio of sine and cosine. This identity particularly useful when dealing with limits involving tangent functions. It helps simplify calculations and provides valuable insights into the behavior of trigonometric functions at their points of discontinuity. Learn more Trig:- What are the Trig Identities?
Lastly, the Exponential Limit Identity: lim(x → 0) (1 + x)^a = 1, vital when dealing with limits involving trigonometric functions raised to a power. It enables the evaluation of limits that would otherwise difficult to solve. By using these trig limit identities, mathematicians and scientists can tackle a wide range of calculus problems involving trigonometric functions with greater ease and efficiency.
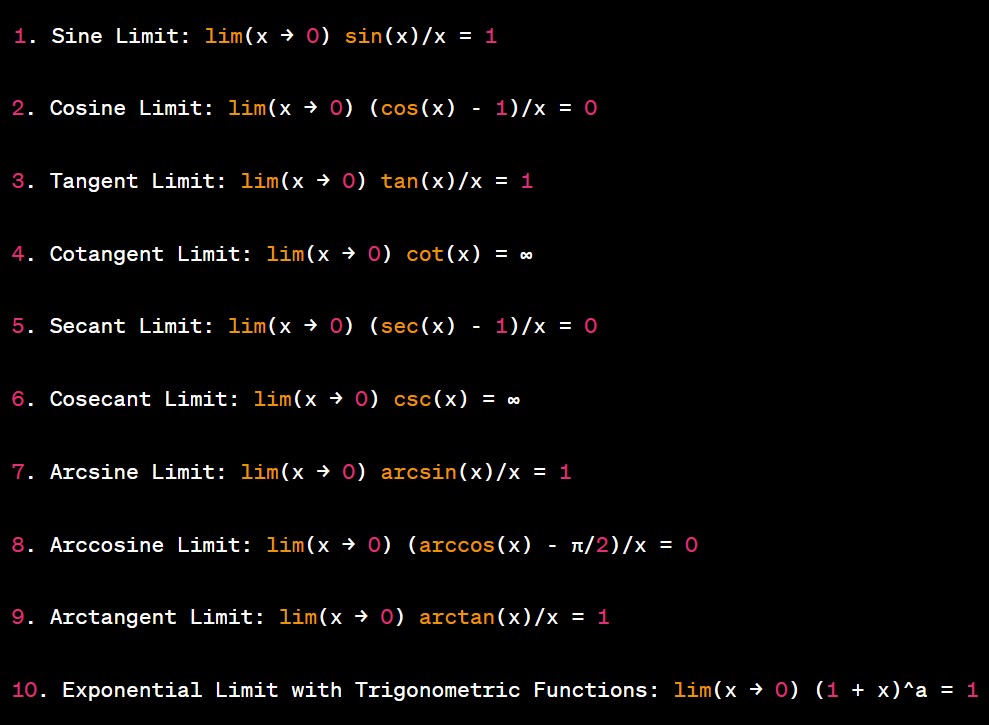
List of Limits for Trigonometric Functions Formulas
Here is a list of essential formulas for evaluating limits of trigonometric functions:
- Sine Limit: lim(x → 0) sin(x)/x = 1. This identity the basis for many trigonometric limit calculations and arises from the geometric interpretation of sine.
- Cosine Limit: lim(x → 0) (cos(x) – 1)/x = 0. This identity often used in conjunction with the Sine Limit to evaluate complex limits involving cosine functions.
- Tangent Limit: lim(x → 0) tan(x)/x = 1. It a key identity for solving limits involving tangent functions and derived from the Sine and Cosine Limits.
- Cotangent Limit: lim(x → 0) cot(x) = ∞. Evaluating the limit of the cotangent function as x approaches 0 demonstrates its vertical asymptote.
- Secant Limit: lim(x → 0) (sec(x) – 1)/x = 0. This formula employed to evaluate limits involving secant functions.
- Cosecant Limit: lim(x → 0) csc(x) = ∞. It shows the vertical asymptote of the cosecant function as x approaches 0.
- Arcsine Limit: lim(x → 0) arcsin(x)/x = 1. This formula is useful when evaluating limits involving the arcsine function.
- Arccosine Limit: lim(x → 0) (arccos(x) – π/2)/x = 0. It is used to calculate limits involving the arccosine function.
- Arctangent Limit: lim(x → 0) arctan(x)/x = 1. This formula is employed to evaluate limits involving the arctangent function.
- Exponential Limit with Trigonometric Functions: lim(x → 0) (1 + x)^a = 1. This general identity is helpful when dealing with limits involving trigonometric functions raised to a power.
These formulas serve as the building blocks for understanding the behavior of trigonometric functions as their inputs approach specific values and invaluable tools for calculus students and mathematicians alike.
Limits Involving Trigonometric Functions
Limits involving trigonometric functions prevalent in calculus and often arise when studying the behavior of functions around certain points. One common limit involving trigonometric functions is the limit of sin(x)/x as x approaches 0. Using the Sine Limit Identity, lim(x → 0) sin(x)/x = 1, we can easily evaluate this limit and find that it equals 1. This result is crucial in various mathematical and scientific applications.
Another frequently encountered limit is the limit of (1 – cos(x))/x as x approaches 0. By applying the Cosine Limit Identity, lim(x → 0) (cos(x) – 1)/x = 0, we find that the limit of (1 – cos(x))/x also evaluates to 0. This type of limit appears in physics, particularly when dealing with harmonic motion and oscillatory systems.
Limits involving tangent functions also essential in calculus. Consider the limit of tan(x)/x as x approaches 0. By using the Tangent Limit Identity, lim(x → 0) tan(x)/x = 1, we can determine that this limit is equal to 1. Such limits encountered when studying derivatives and slopes of curves.
Trigonometric limits become more intricate when combined with other functions. For instance, the limit of (sin(x) + x^2) as x approaches 0 requires both the Sine Limit Identity and basic polynomial limit rules. In such cases, a step-by-step approach is necessary to simplify the expression and evaluate the limit accurately.
Overall, understanding limits involving trigonometric functions is fundamental for various branches of mathematics and sciences. It allows for a deeper comprehension of functions’ behavior near specific points, enabling the analysis of functions’ continuity. Differentiability, and broader mathematical modeling. As such, mastering the techniques to evaluate these limits is crucial for students and professionals in fields such as engineering, physics, and mathematics.