Trig identities form the backbone of trigonometry, enabling us to establish relationships between various trigonometric functions. These identities consist of a collection of fundamental equations that govern the behavior of angles and triangles. In this article, we will delve into the world of trig identities, providing you with an extensive list and explaining their significance. By understanding and applying these identities, you will gain the necessary tools to tackle complex trigonometric calculations with ease.
What are the Trig Identities?
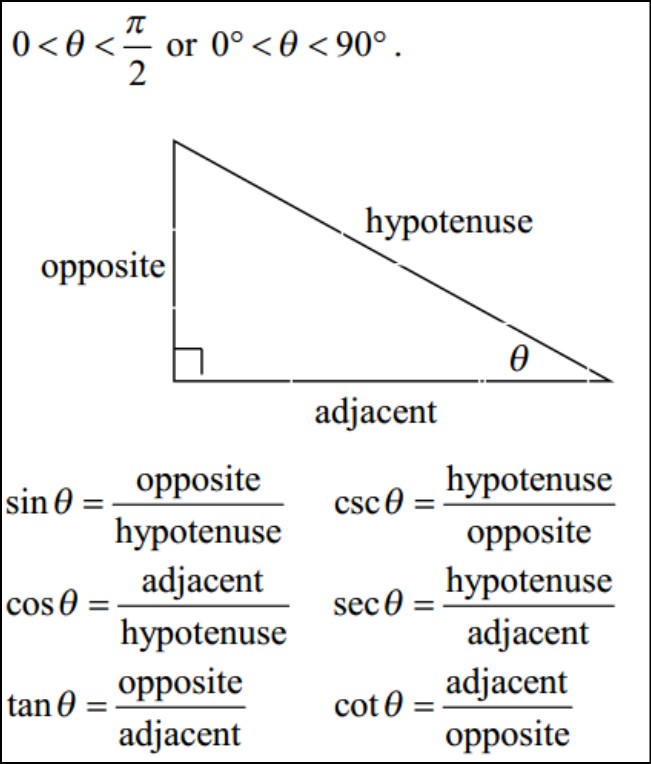
Trigonometric identities are mathematical equations that establish relationships between the trigonometric functions. These identities are useful for simplifying and manipulating trigonometric expressions, solving equations, and proving mathematical statements. Trig identities are derived from the geometric properties of triangles and the unit circle. They allow us to express one trigonometric function in terms of others, which aids in solving complex problems in fields such as physics, engineering, and mathematics.
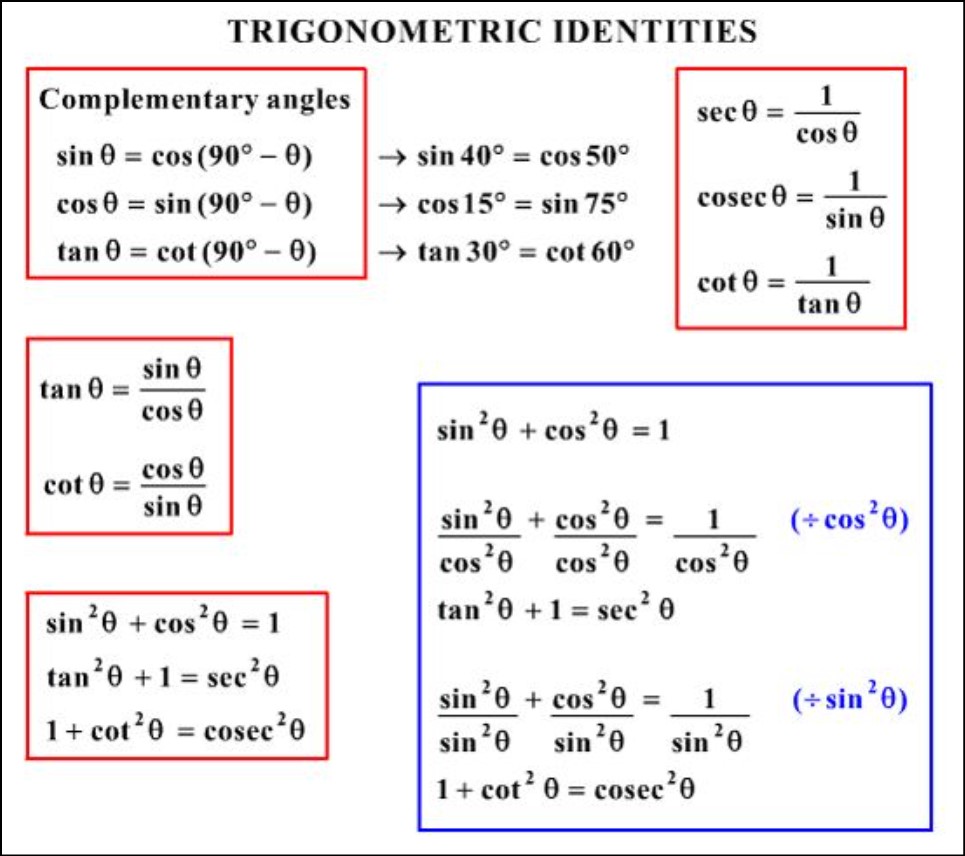
Trig identities can be categorized into several types, including reciprocal identities, Pythagorean identities, quotient identities, and cofunction identities. Reciprocal identities relate the reciprocal functions of a given angle, such as sine and cosecant or cosine and secant. Pythagorean identities are based on the Pythagorean theorem and establish relationships between the three primary trigonometric functions: sine, cosine, and tangent. Quotient identities involve the division of trigonometric functions, such as tangent over cosine or sine over cosine. Cofunction identities link the complementary angles, such as sine and cosine or tangent and cotangent.
By using these trig identities, mathematicians can manipulate trigonometric expressions to simplify them, solve equations involving trigonometric functions, and establish equivalences between different forms of trigonometric expressions. Trig identities provide a powerful toolkit for working with angles, triangles, and periodic functions, enabling the analysis and understanding of a wide range of mathematical and real-world phenomena. Learn more:- Trig Substitution Integration
What Are the 8 Basic Trig Identities?
The eight basic trigonometric identities form the foundation of trigonometry and serve as fundamental relationships between the trigonometric functions. They are derived from the ratios of sides in a right triangle or from the coordinates on the unit circle.
Here are the eight basic trigonometric identities:
- Sine (sin) Identity: sin^2(theta) + cos^2(theta) = 1
- Cosine (cos) Identity: 1 + tan^2(theta) = sec^2(theta)
- Tangent (tan) Identity: 1 + cot^2(theta) = csc^2(theta)
- Cosecant (csc) Identity: csc(theta) = 1 / sin(theta)
- Secant (sec) Identity: sec(theta) = 1 / cos(theta)
- Cotangent (cot) Identity: cot(theta) = 1 / tan(theta)
- Pythagorean Identity: sin^2(theta) + cos^2(theta) = 1
- Reciprocal Identity: csc(theta) = 1 / sin(theta), sec(theta) = 1 / cos(theta), cot(theta) = 1 / tan(theta)
These identities can be used to simplify trigonometric expressions, prove other trigonometric identities, and solve trigonometric equations. They provide a solid starting point for understanding and working with more complex trigonometric concepts and applications.
Full List of Trig Identities
Trigonometric identities encompass a wide range of equations that establish relationships between trigonometric functions.
Here is a comprehensive list of trigonometric identities:
Reciprocal Identities:
- csc(theta) = 1 / sin(theta)
- sec(theta) = 1 / cos(theta)
- cot(theta) = 1 / tan(theta)
Quotient Identities:
- tan(theta) = sin(theta) / cos(theta)
- cot(theta) = cos(theta) / sin(theta)
Pythagorean Identities:
- sin^2(theta) + cos^2(theta) = 1
- 1 + tan^2(theta) = sec^2(theta)
- 1 + cot^2(theta) = csc^2(theta)
Co-function Identities:
- sin(theta) = cos(90° – theta)
- cos(theta) = sin(90° – theta)
- tan(theta) = cot(90° – theta)
- cot(theta) = tan(90° – theta)
- sec(theta) = csc(90° – theta)
- csc(theta) = sec(90° – theta)
Even-Odd Identities:
- sin(-theta) = -sin(theta)
- cos(-theta) = cos(theta)
- tan(-theta) = -tan(theta)
- cot(-theta) = -cot(theta)
Double Angle Identities:
- sin(2theta) = 2sin(theta)cos(theta)
- cos(2theta) = cos^2(theta) – sin^2(theta)
- tan(2theta) = (2tan(theta))/(1 – tan^2(theta))
Sum and Difference Identities:
- sin(theta ± phi) = sin(theta)cos(phi) ± cos(theta)sin(phi)
- cos(theta ± phi) = cos(theta)cos(phi) ∓ sin(theta)sin(phi)
- tan(theta ± phi) = (tan(theta) ± tan(phi))/(1 ∓ tan(theta)tan(phi))
These are just a selection of the numerous trigonometric identities available. Each identity plays a crucial role in different areas of mathematics, physics, engineering, and other fields that rely on trigonometry.
What Is the Point of Trig Identities?
The point of trigonometric identities is to provide mathematical relationships and tools that help simplify and manipulate trigonometric expressions. Trigonometry is used extensively in various fields such as physics, engineering, and mathematics, where angles, triangles, and periodic functions are prevalent.
Trig identities allow us to transform complex trigonometric expressions into simpler forms, making calculations and problem-solving more manageable. They help us establish equivalences between different trigonometric functions and provide alternative representations for trigonometric quantities.
By utilizing trig identities, mathematicians can solve trigonometric equations, prove mathematical statements, and analyze complex systems involving angles and periodic functions. Trig identities also aid in simplifying calculations and making connections between different areas of mathematics.
Moreover, trig identities facilitate the process of solving real-world problems that involve angles, distances, and oscillating phenomena. They provide a systematic and efficient way to model and understand various physical and engineering phenomena, such as waves, vibrations, electrical circuits, and celestial mechanics.