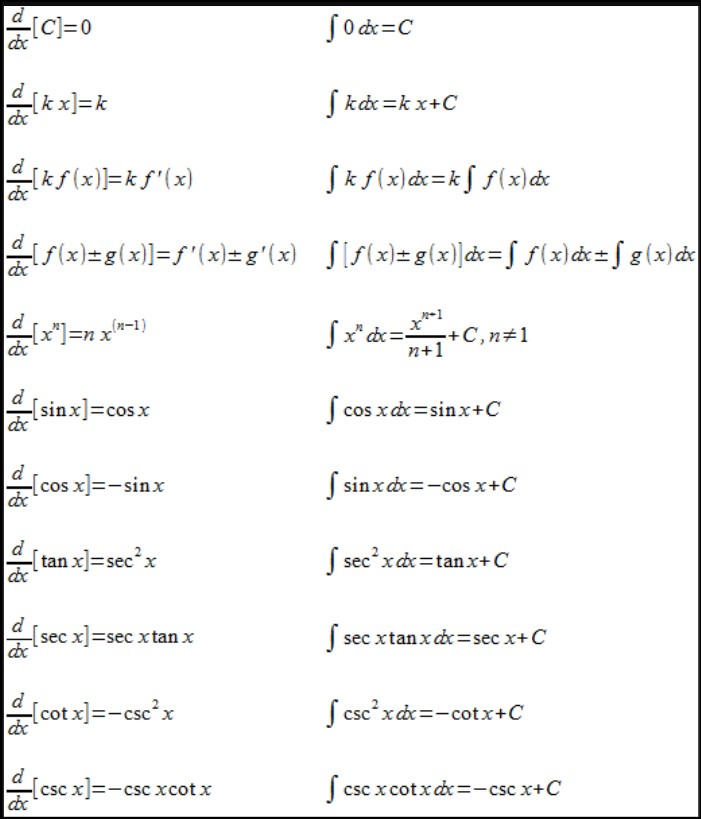The Antiderivative Of Trig Functions, also known as the indefinite integral, is a fundamental concept in calculus that gives the area under a curve.
Antiderivative Of Trig Functions
The antiderivative of trigonometric functions plays a crucial role in calculus and is essential for solving a wide range of mathematical problems. To understand the antiderivative of trig functions, let’s consider the basic trigonometric functions: sine (sin), cosine (cos), and tangent (tan).
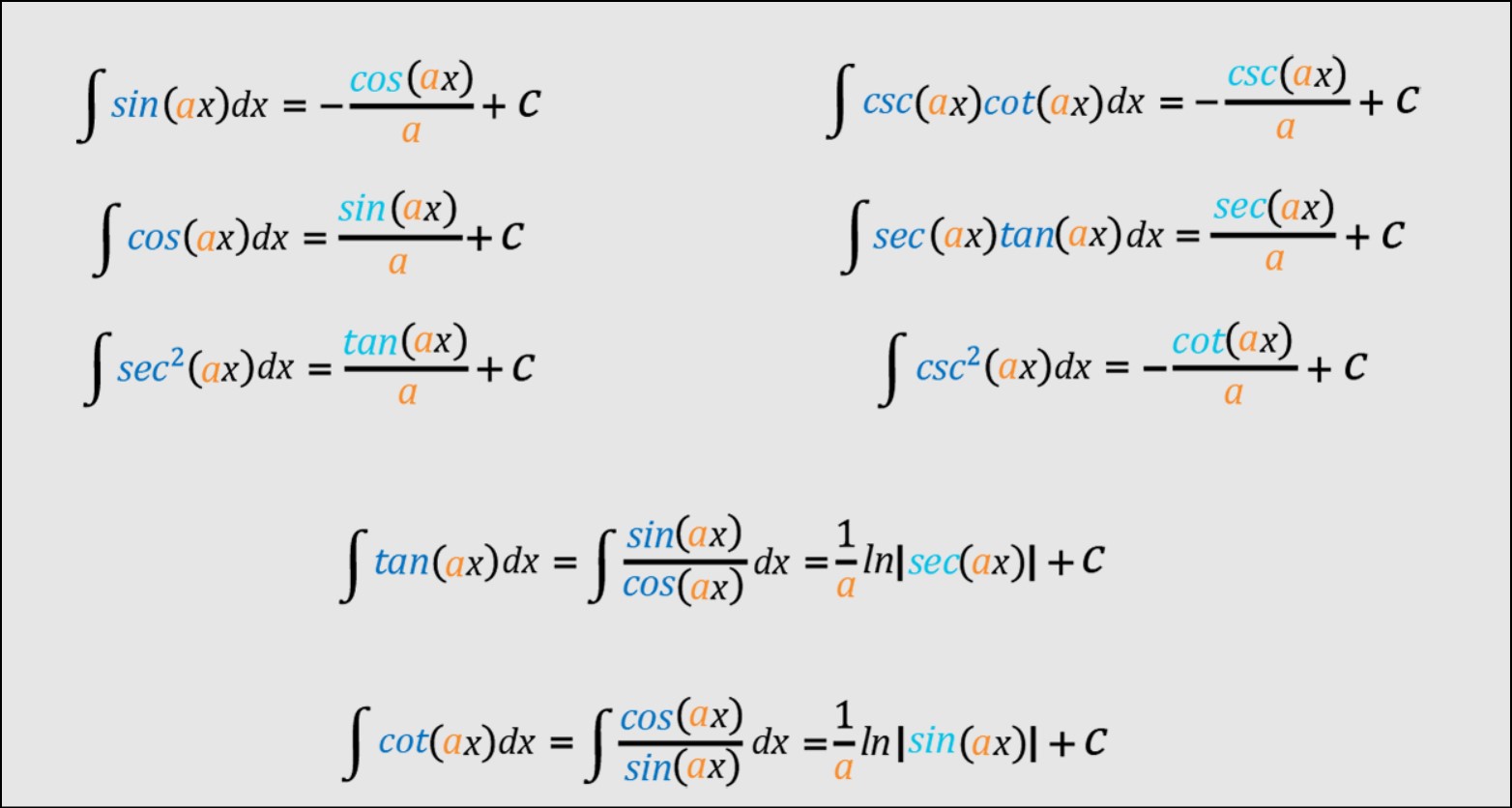
The antiderivative of the sine function (sin x) is determined by taking the negative cosine function (-cos x) plus a constant of integration. Symbolically, ∫sin x dx = -cos x + C, where C represents the constant of integration. This antiderivative relationship highlights the integral’s connection with the cosine function.
Similarly, the antiderivative of the cosine function (cos x) is the sine function (sin x) plus a constant of integration. Thus, ∫cos x dx = sin x + C. This result demonstrates the inverse relationship between the cosine function and its antiderivative, the sine function.
Regarding the tangent function, finding its antiderivative requires a slightly different approach. The antiderivative of the tangent function (tan x) is the natural logarithm of the absolute value of the secant function (ln|sec x|) plus a constant of integration. In symbolic terms, ∫tan x dx = ln|sec x| + C. This antiderivative relationship unveils the connection between the tangent function and the logarithmic function.
In summary, the antiderivative of the trigonometric functions can expressed as follows:
- ∫sin x dx = -cos x + C
- ∫cos x dx = sin x + C
- ∫tan x dx = ln|sec x| + C
Understanding these antiderivative relationships allows us to solve various problems involving trigonometric functions and integrate them into more complex mathematical expressions. Learn more Trigonometry:- Trigonometry Circle Chart
Trigonomerty Antiderivative
The concept of antiderivative in trigonometry is closely tied to the study of calculus and its applications. Trigonometry involves the study of angles and the relationships between angles and the sides of triangles. Antiderivatives, on the other hand, are a fundamental concept in calculus that enables us to find the original function when given its derivative.
When it comes to trigonometry, finding the antiderivative involves working with trigonometric functions such as sine, cosine, tangent, secant, cosecant, and cotangent. The antiderivatives of these functions allow us to determine the original function from its derivative, helping us solve a wide range of mathematical problems.
The antiderivative of trigonometric functions follows a specific set of rules. For example, the antiderivative of the sine function (sin x) is the negative cosine function (-cos x) plus a constant of integration. Conversely, the antiderivative of the cosine function (cos x) is the sine function (sin x) plus a constant of integration.
Similarly, the antiderivative of the tangent function (tan x) is the natural logarithm of the absolute value of the secant function (ln|sec x|) plus a constant of integration. These relationships allow us to find the original functions based on their derivatives, making the study of antiderivatives crucial in trigonometry.
By understanding the antiderivatives of trigonometric functions, we can solve various mathematical problems involving trigonometry more efficiently. Additionally, these concepts have practical applications in fields such as physics, engineering, and signal processing, where trigonometric functions are commonly encountered.
Integration of Trigonometric Functions
The integration of trigonometric functions is a fundamental topic in calculus that allows us to determine the area under the curve of trigonometric functions and solve various mathematical problems. By applying integration techniques, we can find the definite integral or antiderivative of trigonometric functions, providing valuable insights into their behavior and enabling us to solve complex equations involving these functions.
When integrating trigonometric functions, we often encounter different cases depending on the power of the function or the presence of other trigonometric or algebraic factors. For instance, when integrating the basic trigonometric functions, such as sine (sin x) or cosine (cos x), the resulting antiderivative is the opposite of the other trigonometric function plus a constant of integration.
Integration also plays a significant role in solving problems involving trigonometric identities. By manipulating the trigonometric identities and applying integration techniques, we can simplify expressions, evaluate definite integrals, and find solutions to trigonometric equations.
In some cases, the integration of trigonometric functions involves applying specific trigonometric substitutions or employing techniques like integration by parts or partial fraction decomposition. These methods allow us to handle more complex integrals involving trigonometric functions, such as rational trigonometric expressions or higher powers of trigonometric functions.
Overall, the integration of trigonometric functions is a powerful tool that enables us to analyze and solve a wide range of mathematical problems. It is essential for understanding the behavior of trigonometric functions, evaluating areas and volumes, and finding solutions to equations encountered in various fields, including physics, engineering, and mathematics itself.