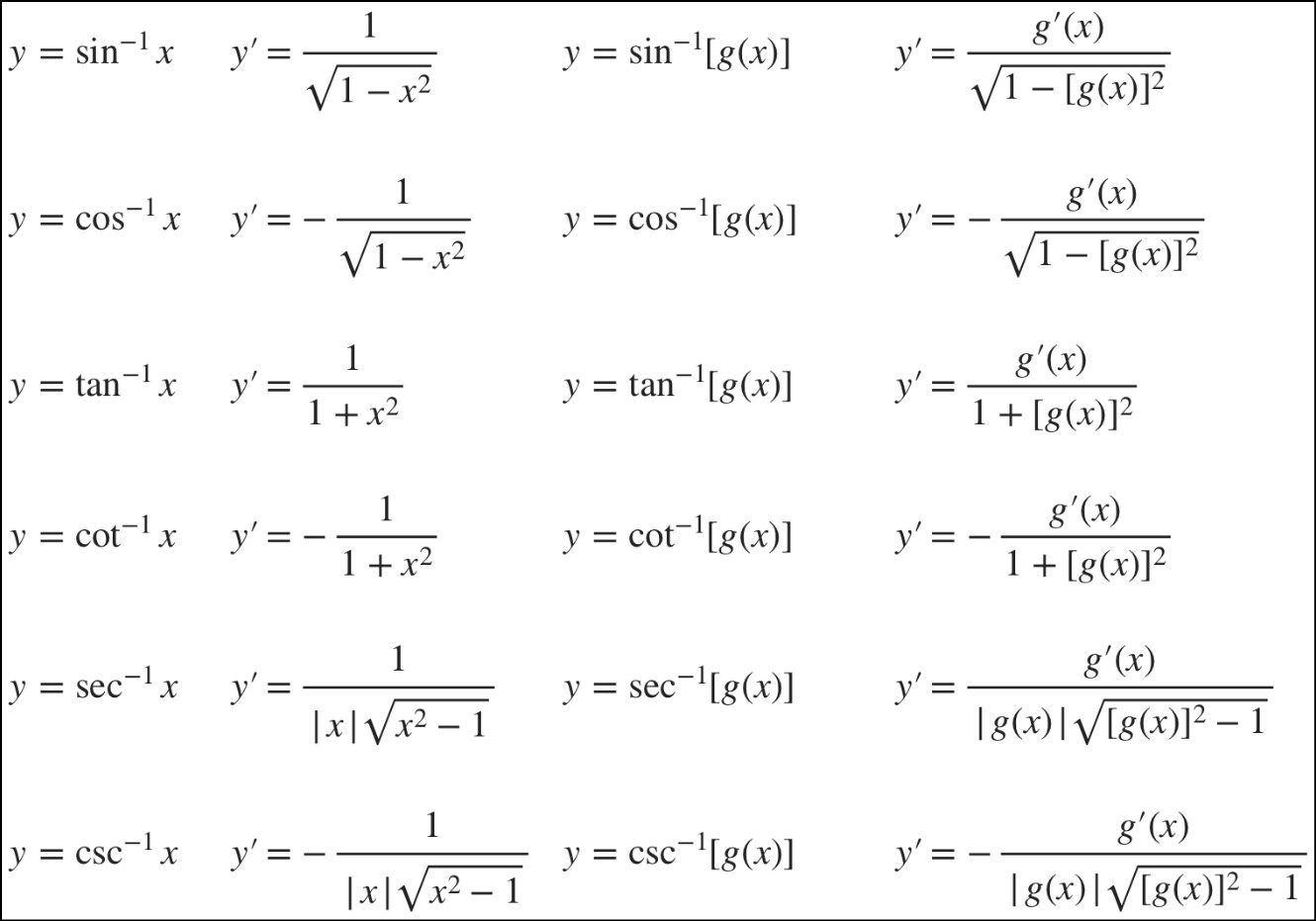Trig Substitution Integration with Examples

Trig Substitution Integration, trigonometric substitution is a technique used in definite and indefinite integration to evaluate integrals of functions containing terms that expressed in terms of trigonometry functions.

Trig Substitution Integration

Trig substitution is a technique used in integration to simplify integrals involving expressions with square roots or quadratic forms. It involves substituting trigonometric functions for certain variables to transform the integral into a more manageable form.

The most commonly used trigonometric substitutions are:

1. Substitution for √(a² – x²): When you have an expression of the form √(a² – x²), where a is a constant and x is the variable, you can use the substitution x = a sinθ or x = a cosθ. This substitution is useful for integrals involving circles or semicircles.

2. Substitution for √(x² + a²): If you encounter an expression of the form √(x² + a²), where a is a constant and x is the variable, you can use the substitution x = a tanθ or x = a secθ. This substitution is helpful for integrals involving hyperbolas or inverse trigonometric functions.

3. Substitution for √(x² – a²): When dealing with an expression like √(x² – a²), where a is a constant and x is the variable, you can use the substitution x = a secθ or x = a cscθ.

After making the appropriate substitution, you apply trigonometric identities and algebraic manipulations to simplify the integral. Once the integral is in a simplified form, you can solve it using techniques like u-substitution, integration by parts, or standard trigonometric integrals.

It’s important to remember to convert any differentials (dx) and limits of integration to match the new variable (θ) introduced by the substitution. Finally, you should replace the original variable (x) with the inverse substitution to obtain the final solution in terms of x.

Other Trigonometry posts:- How to Graph a Trig Function, How to Find Angle In Trigonometry.

Integration with Trig Substitution

Trigonometric substitution a powerful technique used to evaluate integrals involving radical expressions or expressions containing quadratic forms of trigonometric functions.

It is particularly useful when dealing with integrals of the form:

∫f(x, √(a² – x²)) dx or ∫f(x, √(x² + a²)) dx,

where f(x) a rational function or a combination of algebraic and exponential functions.

The idea behind trigonometric substitution to replace the given expression in the integral with a trigonometric function in order to simplify the integral and make it easier to evaluate. There three common trigonometric substitutions:

1. The substitution x = a sin(θ) used when the expression inside the square root of the form (a² – x²).

2. The substitution x = a tan(θ) used when the expression inside the square root of the form (x² + a²).

3. The substitution x = a sec(θ) used when the expression inside the square root of the form (x² – a²).

After making the appropriate trigonometric substitution, you can express all the terms in the integral in terms of θ and then proceed to evaluate the integral using trigonometric identities and techniques. Finally, you must convert back to the original variable using the inverse trigonometric functions.

Performing trigonometric substitution involves the following steps:

1. Identify the appropriate substitution based on the expression inside the square root.
2. Substitute the expression with the trigonometric substitution.
3. Simplify the integral using trigonometric identities.
4. Integrate the simplified expression with respect to the new variable.
5. Convert back to the original variable using inverse trigonometric functions, if necessary.

Integration Inverse Trig Functions

To find the integrals of inverse trigonometric functions, we can use certain trigonometric identities and integration techniques.

The integrals of the inverse trigonometric functions:

1. Integral of arccosine (arccos x): ∫arccos(x) dx = x · arccos(x) + √(1 – x^2) + C

2. Integral of arcsine (arcsin x): ∫arcsin(x) dx = x · arcsin(x) – √(1 – x^2) + C

3. Integral of arctangent (arctan x): ∫arctan(x) dx = x · arctan(x) – 1/2 · ln(1 + x^2) + C

4. Integral of arcsecant (arcsec x): ∫arcsec(x) dx = x · arcsec(x) – ln|x + √(x^2 – 1)| + C

5. Integral of arccosecant (arccsc x): ∫arccsc(x) dx = x · arccsc(x) + ln|x + √(x^2 – 1)| + C

6. Integral of arccotangent (arccot x): ∫arccot(x) dx = x · arccot(x) + 1/2 · ln(1 + x^2) + C

These formulas useful when integrating functions involving inverse trigonometric functions. Remember to always include the constant of integration (C) when finding indefinite integrals.