A trigonometry circle chart is a visual representation of the unit circle, which is a circle with a radius of 1. The unit circle is used in trigonometry to help illustrate the relationships between the angles and the lengths of the sides of right triangles.
Trigonometry Circle Chart
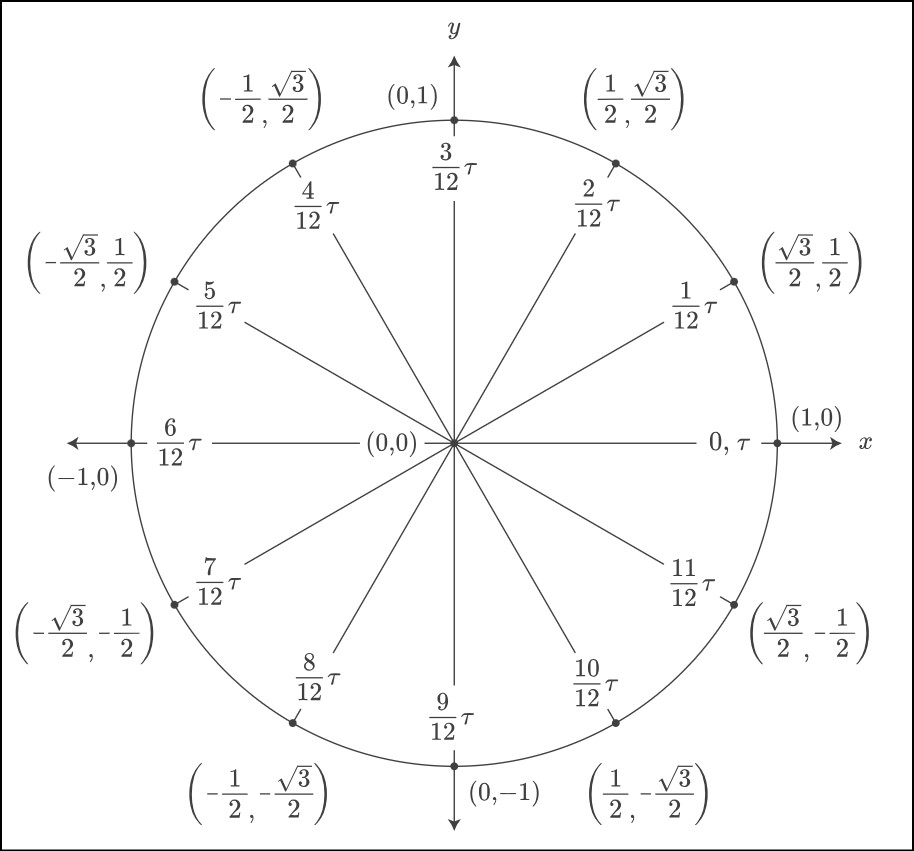
A trigonometry circle chart, also known as a unit circle, is a valuable tool used in the study of trigonometry. It provides a visual representation of the relationship between angles and the trigonometric functions sine, cosine, and tangent. The circle chart is centered at the origin of a coordinate plane and has a radius of 1 unit. The circumference of the circle is divided into angles measured in degrees or radians, enabling students to easily identify the values of trigonometric functions for specific angles.
The trigonometry circle chart is divided into four quadrants, each representing different angles. The angles are measured from the positive x-axis in a counterclockwise direction. The x-coordinate of a point on the circle corresponds to the cosine of the angle, while the y-coordinate represents the sine. For example, the point (1, 0) corresponds to an angle of 0 degrees or 0 radians, where the cosine is 1 and the sine is 0. The chart allows students to quickly determine the trigonometric values for various angles without the need for complex calculations.
By utilizing the trigonometry circle chart, students can solve trigonometric equations, identify the values of trigonometric functions for specific angles, and understand the properties of these functions more easily. It serves as a fundamental tool in trigonometry, laying the groundwork for advanced concepts such as the unit circle, trigonometric identities, and the relationship between angles and triangles.
The chart’s visual representation helps students visualize the periodicity and symmetry of trigonometric functions, enabling them to better grasp the concepts and apply them to real-world problems. Learn more about Trigonometry:- Trigonometry Quadrant
Circle in Trigonometry
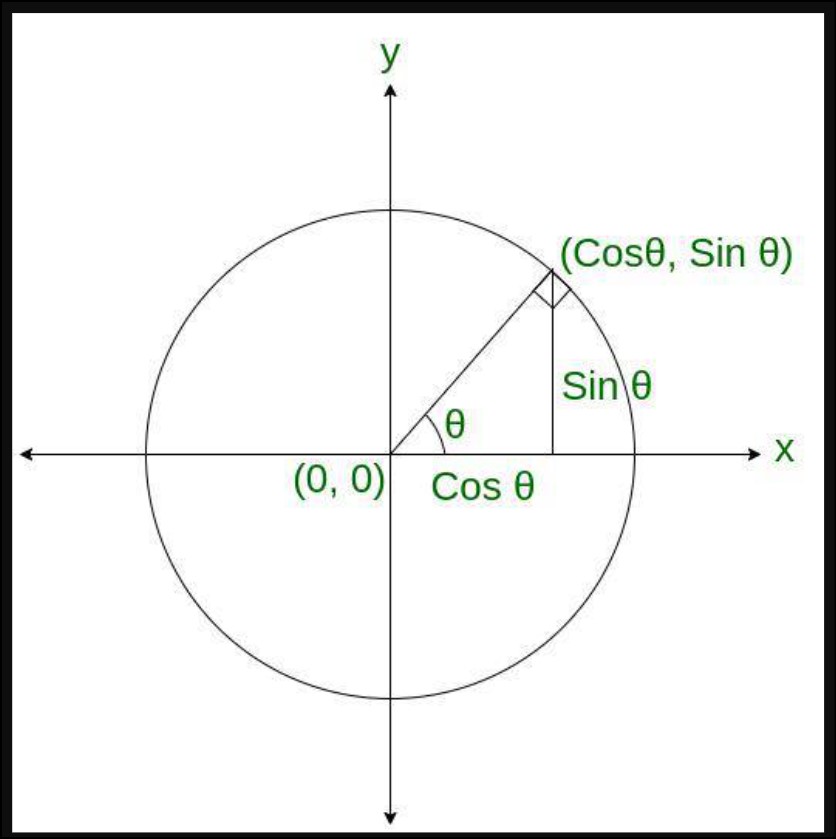
In trigonometry, the concept of a circle plays a crucial role in understanding the relationships between angles, coordinates, and trigonometric functions. A circle is defined as a set of points equidistant from a central point, forming a perfectly round shape. Within the context of trigonometry, the unit circle is particularly important. It is a circle with a radius of 1 unit and is often used to define the values of trigonometric functions for various angles.
The unit circle in trigonometry is typically centered at the origin of a coordinate plane. This allows for easy visualization and calculation of trigonometric values based on the coordinates of points on the circle. The circumference of the unit circle is divided into angles measured in degrees or radians, enabling precise determination of trigonometric values for specific angles.
By examining the relationship between angles and points on the unit circle, trigonometric functions such as sine, cosine, and tangent can be defined. The x-coordinate of a point on the circle corresponds to the cosine of the angle, while the y-coordinate represents the sine. Tangent, on the other hand, is defined as the ratio of sine to cosine.
Understanding the circle in trigonometry is crucial for solving trigonometric equations, working with triangles, and analyzing periodic functions. The unit circle provides a standardized reference point for determining trigonometric values, allowing for consistency and accuracy in calculations. By utilizing the properties and coordinates of the unit circle, students can easily identify the values of trigonometric functions for any angle, making complex calculations more manageable.
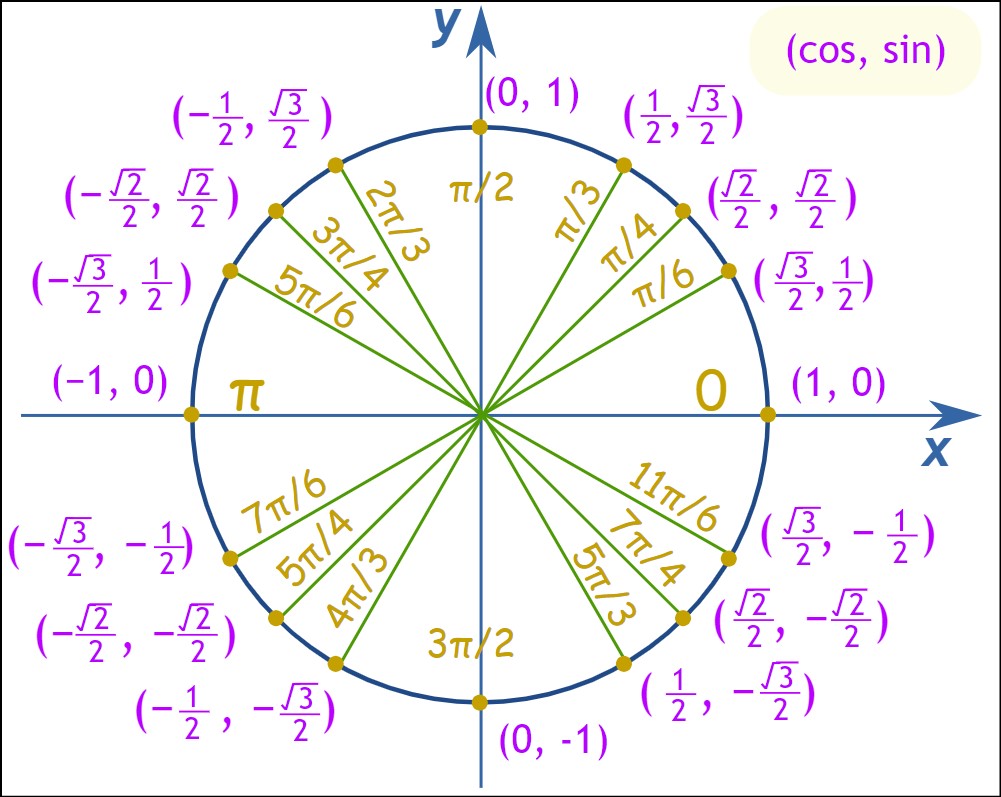
Unit Circle Chart Labeled With Special Angles And Values
A unit circle chart labeled with special angles and values is an essential reference tool in trigonometry. The unit circle, with a radius of 1 unit, is divided into angles measured in degrees or radians. These angles correspond to specific trigonometric values such as sine, cosine, and tangent, which are labeled on the chart. The labeled chart helps students quickly identify the trigonometric values for commonly used angles, often referred to as “special angles.”
The special angles on the unit circle chart typically include 0 degrees, 30 degrees, 45 degrees, 60 degrees, and 90 degrees. These angles correspond to key points on the unit circle, which have predetermined values for sine, cosine, and tangent. For example, at 0 degrees, the sine value is 0, the cosine value is 1, and the tangent value is 0. As the angles increase, the values change accordingly, following the patterns established by the trigonometric functions.
By referring to a unit circle chart labeled with special angles and values, students can easily determine the trigonometric values for these angles without the need for complex calculations. It serves as a handy guide, saving time and promoting accuracy in solving trigonometric equations or evaluating trigonometric functions for specific angles. The labeled chart also helps students develop a deeper understanding of the relationships between angles and trigonometric values.
Moreover, the unit circle chart with labeled special angles and values is particularly useful when dealing with right triangles. Since right triangles have angles of 30 degrees, 45 degrees, and 60 degrees, the labeled chart enables students to quickly identify the exact values of sine, cosine, and tangent for these angles. This knowledge can be applied in a variety of real-world scenarios, such as calculating distances, measuring heights, or analyzing the properties of triangles.