The Basic 8 Trig Identities Worksheet with Answers offers a valuable resource for students and enthusiasts looking to master trigonometry. Trigonometric identities play a crucial role in solving complex mathematical problems involving angles and triangles. This worksheet provides a collection of practice questions, accompanied by step-by-step solutions, allowing you to reinforce your knowledge of the eight fundamental trigonometric identities. Strengthen your understanding of trigonometry and enhance your problem-solving skills with this comprehensive worksheet.
The Basic 8 Trig Identities
Trigonometric identities are equations that relate the angles and lengths of triangles to the values of trigonometric functions. The basic 8 trig identities are foundational equations that play a crucial role in solving trigonometric problems and proving more complex identities. These identities are derived from the ratios of the sides of right triangles and are used extensively in trigonometry and calculus.
The first four basic trig identities involve the three primary trigonometric functions: sine (sin), cosine (cos), and tangent (tan). The remaining four identities are derived from the reciprocal functions: cosecant (csc), secant (sec), and cotangent (cot).
The basic 8 trig identities are as follows:
- Pythagorean Identities:
- sin²θ + cos²θ = 1
- 1 + tan²θ = sec²θ
- 1 + cot²θ = csc²θ
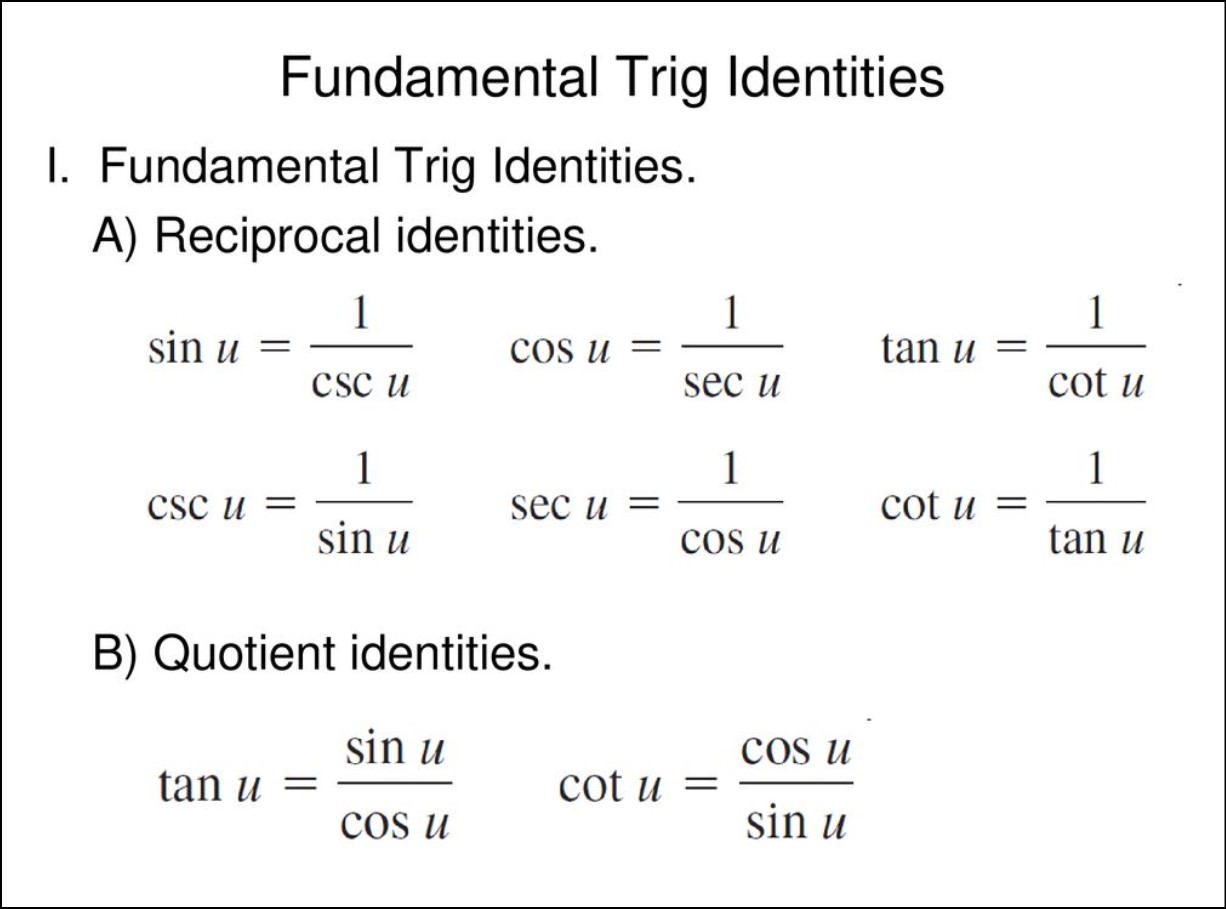
- Reciprocal Identities:
- cscθ = 1/sinθ
- secθ = 1/cosθ
- cotθ = 1/tanθ
- Quotient Identities:
- tanθ = sinθ/cosθ
- cotθ = cosθ/sinθ
These identities are used to simplify trigonometric expressions, solve equations, and manipulate trigonometric functions. Understanding and memorizing these identities are fundamental for success in trigonometry and its applications. Learn more:- Antiderivative Of Trig Functions
Eight Fundamental Trigonometric Identities
Trigonometric identities are mathematical equations that establish relationships between the angles and lengths of triangles and the values of trigonometric functions. The eight fundamental trigonometric identities form the basis for more complex trigonometric identities and equations. These identities are derived from the ratios of the sides of right triangles and are widely used in various branches of mathematics, physics, and engineering.
The fundamental trigonometric identities are divided into two categories: the Pythagorean identities and the reciprocal identities.
Pythagorean Identities:
- sin²θ + cos²θ = 1
- 1 + tan²θ = sec²θ
- 1 + cot²θ = csc²θ
Reciprocal Identities: 4. cscθ = 1/sinθ
- secθ = 1/cosθ
- cotθ = 1/tanθ
The Pythagorean identities relate the squares of sine, cosine, and tangent to each other, while the reciprocal identities express the trigonometric functions in terms of their reciprocals. These identities enable the simplification of trigonometric expressions, the solution of trigonometric equations, and the conversion between different trigonometric functions.
By understanding and applying these fundamental trigonometric identities, mathematicians and scientists can analyze and solve a wide range of problems involving angles, triangles, and periodic phenomena.
Basic 8 Trig Identities Worksheet with Answers
Below is a worksheet that provides practice problems for the basic 8 trig identities. Use the given identities to simplify the trigonometric expressions and write the answers in terms of sine, cosine, and tangent functions.
- Simplify the expression: sin²θ + cos²θ
Answer: 1
- Simplify the expression: 1 + tan²θ
Answer: sec²θ
- Simplify the expression: 1 + cot²θ
Answer: csc²θ
- Simplify the expression: cscθ * sinθ
Answer: 1
- Simplify the expression: secθ * cosθ
Answer: 1
- Simplify the expression: cotθ * tanθ
Answer: 1
- Simplify the expression: sinθ / cosθ
Answer: tanθ
- Simplify the expression: cosθ / sinθ
Answer: 1/tanθ
By practicing these problems, you will become more familiar with the basic 8 trig identities and gain confidence in using them to simplify and manipulate trigonometric expressions.
What Are the Basic Trigonometric Identities?
The basic trigonometric identities are a set of fundamental equations that relate the angles and lengths of triangles to the values of trigonometric functions. These identities are derived from the ratios of the sides of right triangles. And serve as the building blocks for more complex trigonometric equations and formulas. The basic trigonometric identities include:
- Pythagorean Identities:
- sin²θ + cos²θ = 1: This identity states that the square of the sine of an angle plus the square of the cosine of the same angle equals 1.
- 1 + tan²θ = sec²θ: This identity states that the square of the tangent of an angle plus 1 equals the square of the secant of the same angle.
- 1 + cot²θ = csc²θ: This identity states that the square of the cotangent of an angle plus 1 equals the square of the cosecant of the same angle.
- Reciprocal Identities:
- cscθ = 1/sinθ: This identity states that the cosecant of an angle is equal to the reciprocal of the sine of the same angle.
- secθ = 1/cosθ: This identity states that the secant of an angle is equal to the reciprocal of the cosine of the same angle.
- cotθ = 1/tanθ: This identity states that the cotangent of an angle is equal to the reciprocal of the tangent of the same angle.
- Quotient Identities:
- tanθ = sinθ/cosθ: This identity states that the tangent of an angle is equal to the ratio of the sine of the angle to the cosine of the same angle.
- cotθ = cosθ/sinθ: This identity states that the cotangent of an angle is equal to the ratio of the cosine of the angle to the sine of the same angle.s